D - 地図が2枚
解説
 /
/ 
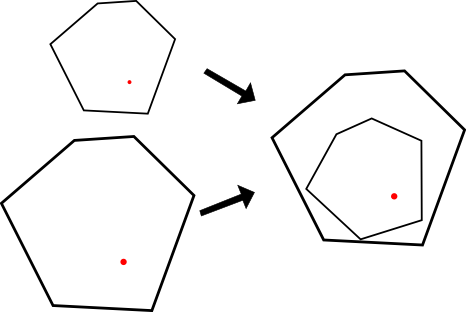
右の状態で2つの地図が与えられる.赤い点が求める点.
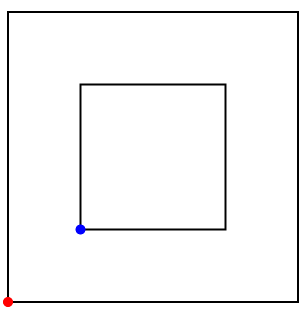
入力の多角形の図.赤い点が (x_{11}, y_{11}) で青い点が (x_{21}, y_{21}) に対応する.
 /
/ 
実行時間制限: 2 sec / メモリ制限: 256 MiB
問題
2枚の異なる縮尺の日本地図を重ねると,同じ地点が重なる点が必ずできる.
地図 A とそれを縮小した地図 A' を用意し, A' を A からはみ出さないように置く. そうすると, A の点 p と, A' で p に対応する点 p' が同じ位置にくるような p がただ一つ存在するのである!
凸多角形の地図 A と,それを半分に縮小&回転&平行移動してもとの地図に真におさまるようにした地図 A' が,二次元空間の座標で与えられる. 地図 A でも A' でも同じ地点(上の p と p')を示しているような点の座標を求めよ.

右の状態で2つの地図が与えられる.赤い点が求める点.
入力
n
x_{11} y_{11}
...
x_{1n} y_{1n}
x_{21} y_{21}
...
x_{2n} y_{2n}
1行目に多角形の頂点数 n が与えられる. 続く n 行に大きい多角形の頂点座標が反時計回りで与えられる. 続く n 行に縮小後の多角形の頂点座標が反時計回りで与えられる. (x_{1k}, y_{1k}) は (x_{2k}, y_{2k}) に対応している.
出力
求める点の座標を x, y の順で空白で区切って1行に出力せよ.絶対誤差 10^{-6} まで許容する.
制約
- 地図は自己交差のない凸な単純多角形と仮定してよい.
- 縮小後の多角形の座標はすべて元の多角形の内部にある.
- 縮小は常に1/2倍
- 3 \leq n \leq 20.
- 0 \leq x_{1k}, y_{1k}, x_{2k}, y_{2k} \leq 100.
- 縮小前の多角形の辺の長さは全て1以上と仮定してよい.
- 縮小後の多角形の座標は,実際の座標を小数点以下9桁で打ち切ったものが与えられる.
部分点
この問題の判定には,50点分のテストケースのグループが設定されている. このグループに含まれるテストケースの入力は以下の条件を満たす.
- n = 4
- (x_{11},y_{11}) = (0,0)
- (x_{12},y_{12}) = (100,0)
- (x_{13},y_{13}) = (100,100)
- (x_{14},y_{14}) = (0,100)
- (x_{22},y_{22}) = (x_{21}+50,y_{21})
- (x_{23},y_{23}) = (x_{21}+50,y_{21}+50)
- (x_{24},y_{24}) = (x_{21},y_{21}+50)
入力例 1
4 0 0 100 0 100 100 0 100 25 25 75 25 75 75 25 75
入力例 1 に対する出力例
50.000000000 50.000000000

入力の多角形の図.赤い点が (x_{11}, y_{11}) で青い点が (x_{21}, y_{21}) に対応する.
入力例 2
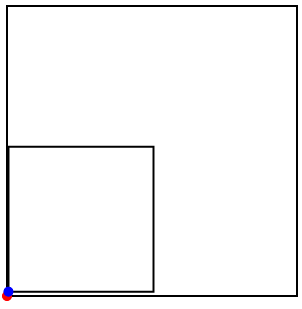
4 0 0 100 0 100 100 0 100 0.5 1.5 50.5 1.5 50.5 51.5 0.5 51.5
入力例 2 に対する出力例
1.000000000 3.000000000

入力例 3
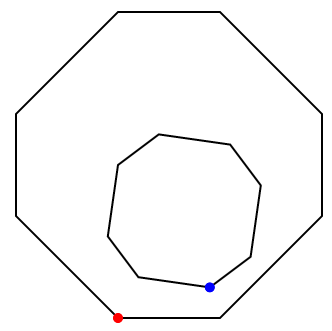
8 2.0 1.0 3.0 1.0 4.0 2.0 4.0 3.0 3.0 4.0 2.0 4.0 1.0 3.0 1.0 2.0 2.9 1.3 3.3 1.6 3.4 2.3 3.1 2.7 2.4 2.8 2.0 2.5 1.9 1.8 2.2 1.4
入力例 3 に対する出力例
3.0 2.0
