H - Huge Kingdom: Atcoder
解説
 /
/ 
この問題はマラソン問題です。
writer解が必ずしも満点であるとは限りません。できるだけ良い点数を取りましょう。
配点: $1500$ 点
また、その王国は連結であります。つまり「木」です。
あなたは、その王国の構造を当てなければなりません。
ここでいう構造というのは、それぞれの道がどの番号の街とどの番号の街をつないでいるのか、という事です。
さて、あなたは構造を当てるにおいて、以下のような質問ができます。
 その時、できるだけ少ない質問回数で王国の構造を当てなさい。
その時、できるだけ少ない質問回数で王国の構造を当てなさい。
最初、以下のように入力される。
次に、あなたは以下の様な質問をすることができる。
質問は、以下のような形式ですることができる。
また、質問は、以下のように返される。
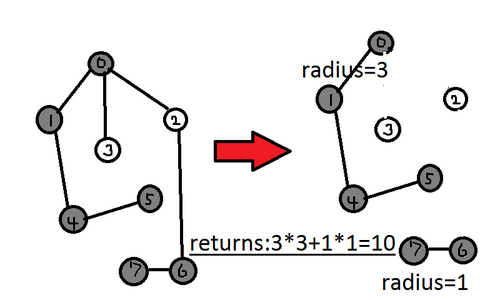
グラフ$G$の各連結成分についての、「木の直径」を2乗した値の総和が返される。
最後に、あなたは以下のような出力をしなければならない。
$(a_i,b_i)$は、街$a_i$と街$b_i$を直接つなぐ道があることを示す。
ただし、出力する道の順番はどのようなものでも良い。また、それぞれの道を出力する方法は2通りあるが、【(1,2),(2,1)など】その出力の順番もどれでもよい。
ケースは5個あるので、得点は理論値を$5$で割った値になる。
その王国は、以下の図のような構造をしています。
ただし, 必ずしも意味のある質問をしているとは限らない。
また, これらの情報で必ずしも盤面が把握できるとは限らず, エスパーをすることも許されます。
 /
/ 
実行時間制限: 4 sec / メモリ制限: 256 MiB
問題文
Atcoder王国は、$N$個の街と$N-1$個の道から成り立っています。また、その王国は連結であります。つまり「木」です。
あなたは、その王国の構造を当てなければなりません。
ここでいう構造というのは、それぞれの道がどの番号の街とどの番号の街をつないでいるのか、という事です。
さて、あなたは構造を当てるにおいて、以下のような質問ができます。
- 文字列$S$($N$文字)を出力する。その時、$S_i$=1の時、$i$番目の街を黒く塗り、$S_i$=0の時、$i$番目の街を白く塗ることを意味する。
- $N$頂点のグラフ$G$を考える。
- 王国の道の両端の街が、両方とも黒く塗られている場合、グラフ$G$にその辺を追加する。
- グラフ$G$の各連結成分についての、「木の直径」を2乗した値の総和が返される。

入出力
これはリアクティブ問題である。最初、以下のように入力される。
$N$
- 1行に、Atcoder王国の街の個数$N$が与えられる。
次に、あなたは以下の様な質問をすることができる。
質問は、以下のような形式ですることができる。
? $S$$S$は、質問する文字列(=街の塗り方)である。$S$は$N$文字でなければならない。
また、質問は、以下のように返される。
$d$質問で出力された文字列$S$について、問題文で与えられた作り方でグラフ$G$を作る。
グラフ$G$の各連結成分についての、「木の直径」を2乗した値の総和が返される。
最後に、あなたは以下のような出力をしなければならない。
! $(a_1,b_1)$ $(a_2,b_2)$ $(a_3,b_3)$ … $(a_{N-1},b_{N-1})$それは、Atcoder王国の構造を突き止めたことを示す。
$(a_i,b_i)$は、街$a_i$と街$b_i$を直接つなぐ道があることを示す。
ただし、出力する道の順番はどのようなものでも良い。また、それぞれの道を出力する方法は2通りあるが、【(1,2),(2,1)など】その出力の順番もどれでもよい。
制約
- $N$ = $200$
- Atcoder王国には$N-1$本の道があり、連結である
- Atcoder王国の街の番号は$0$以上$N-1$以下である。(0-based)
- ケースはランダムに作られた。
テストケースの生成方法
以下の操作を、街が全て連結(連結成分が1つ)になるまで繰り返す。- ランダムな街の番号$u$, $v$を選ぶ。
- もし、今の状態で街$u$から街$v$まで、いくつかの道路を使ってたどり着けない場合、街$u$と$v$の間に道路を結ぶ。
- そうでない場合、何もしない。最初の操作に戻る。
得点
あなたが質問した回数を$L$とする。その時得点の理論値は以下のようになる。- $L > 20000$の時、$0$点
- $18000 < L ≦ 20000$の時、$200$点
- $5000 < L ≦ 18000$の時、$650-L/40$点
- $4000 < L ≦ 5000$の時、$800-L/20$点
- $2000 < L ≦ 4000$の時、$1400-L/5$点
- $1200 < L ≦ 2000$の時、$1500-L/4$点
- $700 < L ≦ 1200$の時、$1850-L/2$点
- $L ≦ 700$の時、$1500$点
ケースは5個あるので、得点は理論値を$5$で割った値になる。
入力例
このケースは、$N=4$である。実際のケースではそのようなものは存在しない。(制約を満たしていないため)N=4 0 1 1 2 1 3
出力例
以下、やりとりの例である。| プログラムへの入力 | プログラムの出力 |
|---|---|
| 4 | |
| ? 1111 | |
| 4 | |
| ? 1101 | |
| 4 | |
| ? 1001 | |
| 0 | |
| ? 1100 | |
| 1 | |
| ? 1011 | |
| 0 | |
| ! (0,1) (1,2) (1,3) |
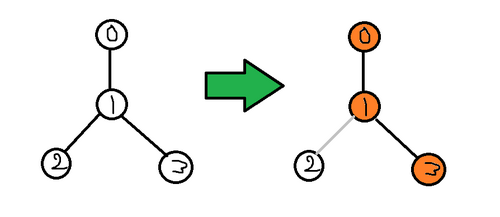
その王国は、以下の図のような構造をしています。

ただし, 必ずしも意味のある質問をしているとは限らない。
また, これらの情報で必ずしも盤面が把握できるとは限らず, エスパーをすることも許されます。