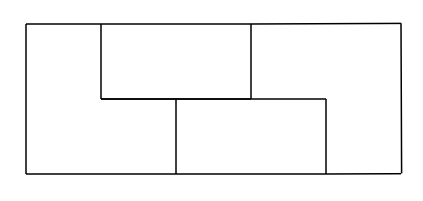
タイル \(L\) は、以下のように \(2\) 枚同時に使い間をタイル \(I\) で埋めるような構成でしか使えません。

上記のような構成は、横幅が \(3\) 以上の時は上下を反転する \(2\) 通りが、\(2\) 以下の時は \(0\) 通りがあります。

全体を見ると、このパーツを \(\displaystyle \frac{A}{2}\) 個使い、その間にタイル \(I\) だけを入れるという形になります。

タイル \(I\) のみで \(2 \times N\) を埋める方法はフィボナッチ数となります。

より \(\displaystyle f(x)=\sum_{i=3}^{\infty} 2x^i,g(x)=\frac{1}{1-x-x^2}\) とした時、解は \(f(x)^{\frac{A}{2}}g(x)^{\frac{A}{2}+1}\) の \(x^N\) の係数となります。

係数が \(0\) でない項が \(M\) 個である形式的冪級数 \(f(x)\) に対し、\(f(x)^n\) の先頭 \(N\) 項は \(O(NM)\) で求めることができます（参考 : https://codeforces.com/blog/entry/76447）。このテクニックを用いることで、本問題を \(O(N)\) で解くことができます。