F - rng_58's Last Problem 解説 by rng58_admin
It requires really lots of steps of observation despite of its very simple setting (the main part of the statement is just one line). Congratulations to contestants who solved it during the contest!
In this editorial, in order not to make it messy, we use diagrams and examples, but it works in general.
Let’s use the following diagram to represent the movements of the sand. The horizontal position represents the amount of sand in some specific bulb of the \(1\)-second sandglass, and the vertical position is a similar thing for the \(\sqrt{2}\)-second sandglass.

Then, for example, the strategy described in the statement corresponds to the path \(A - E - F - C\). In general, we start from \(A\), and whenever we “hits” a wall we can change the velocity vector. The velocity vector can be one of \((-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1, 1)\).
What strategies are possible on this diagram? After we start \(A\), we have three choices of directions. In case we go towards \(B\), after \(1\) second we reach \(B\) and that’s essential the same position as \(A\). A similar thing happens when we go towards \(C\). This means that we can always add \(1\) or \(\sqrt{2}\) to a measurable time and we get another measurable time.
The most interesting case is when we go towards \(E\). In this case we have five possible directions next. In two of them we go to \(B\) or \(C\) next and we reach a corner. In one of them we go to the opposite side of \(E\) (shown in the dot line, that is essentially the same position as \(E\)), but this just adds \(1\) to the time and we can ignore this movement. In the other two of them we go to \(A\) or \(F\) - keep staying on the “diagonal” part.
In general, we have a diagonal line (\(A - E - F - G - H - I - J - K - L - M - \cdots\)). After we start \(A\), we go back and forth on this diagonal, and at some time we finally decide to go to a corner.
Let’s expand the diagonal line as follows:
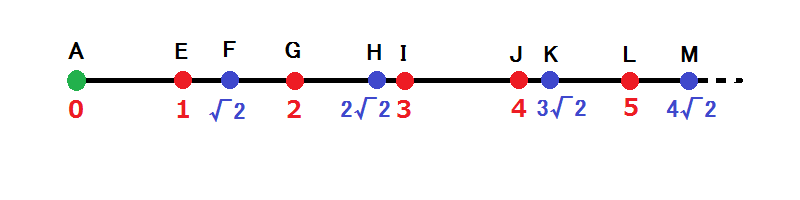
Now the strategy can be described as follows. We start from \(A\) on this number line. Then we can move back and forth on this line, and an event happens when we reach a point. When we reach a point, we may change the direction, or jump to \(A\).
(To clarify - we can’t jump to \(A\) after \(A - E - F - G\) or \(A - E - F - E\) for example, but \(A - E - F - D\) and \(A - E - F - C\) have the same lengths and we can use them instead.)
What are possible lengths of a walk on this number line? See the following diagram showing \(A - G - E - I - H - M - L - M - J\) as an example:

This can be decomposed into \(A - M - J\), plus some even number of short segments. The same happens even when some jumps are involved:
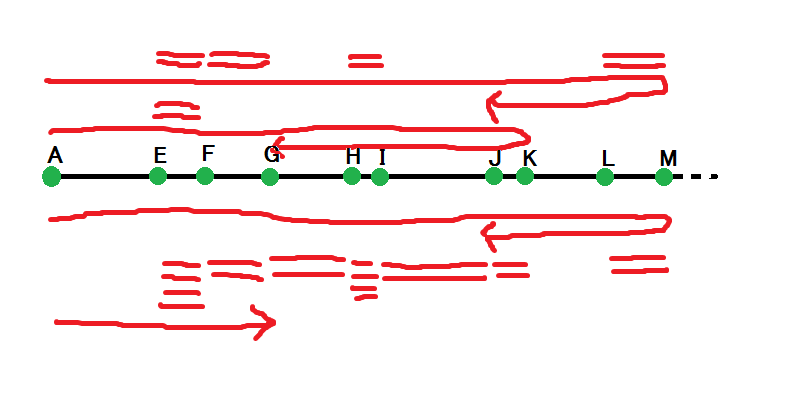
That is, a valid strategy can be always decomposed into \(A - ? - ?\), plus even number of short segments, plus some multiples of \(1\) and \(\sqrt{2}\).
Formally speaking, \(T\) is measurable if \(T\) has the following representation. Here \(z_0, z_1, z_2, z_3, \cdots = 0, 1, \sqrt{2}, 2, \cdots\) are all multiples of \(1\) and \(\sqrt{2}\), sorted in an increasing order.
\(T = 2 z_q - z_p +2 \{ \sum_{i=0}^{q-1} c_i (z_{i+1} - z_i) \} + r + s \sqrt{2}\)
where \(0 \leq p \leq q, 0 \leq r\), \(0 \leq s\), and \(0 \leq c_i\) are some integer coefficients. \(z_q\) corresponds to the furthest point we reach, \(z_p\) corresponds to the point of the goal, and the sigma part corresponds to a collection of short segments.
Next, let’s think about the sigma part. For a fixed \(q\), what are possible values of this part? For example, when \(z_q = M\), we are interested in possible values we can get as a sum of lengths of some subintervals between \(A\) and \(M\).
In the following diagram, a point \((x, y)\) corresponds to the value \(x + y \sqrt {2}\). The green diagonal line corresponds to \(x + y \sqrt{2} = 0\), and other two green lines correpond to \(x = z_q, y \sqrt {2} = z_q\). The red points show possible lengths of one subinterval. What values can be a sum of some red points?
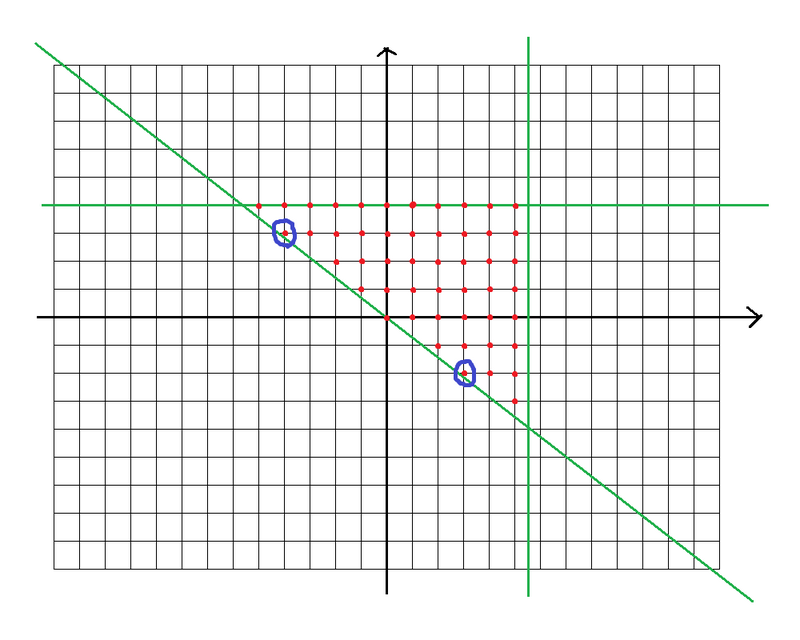
It turns out that the two blue-circled points are important, that is, the points with the largest slopes from the origin. Draw two half-lines from the origin to each of the blue point, and the region above these two half-lines is a possible region. For example, in the following diagram, the red point \((-10, 8)\) can be written as \(2\) times the blue point, plus \((-2, 2)\) (and the same strategy always works for all points in the “Possible” region).
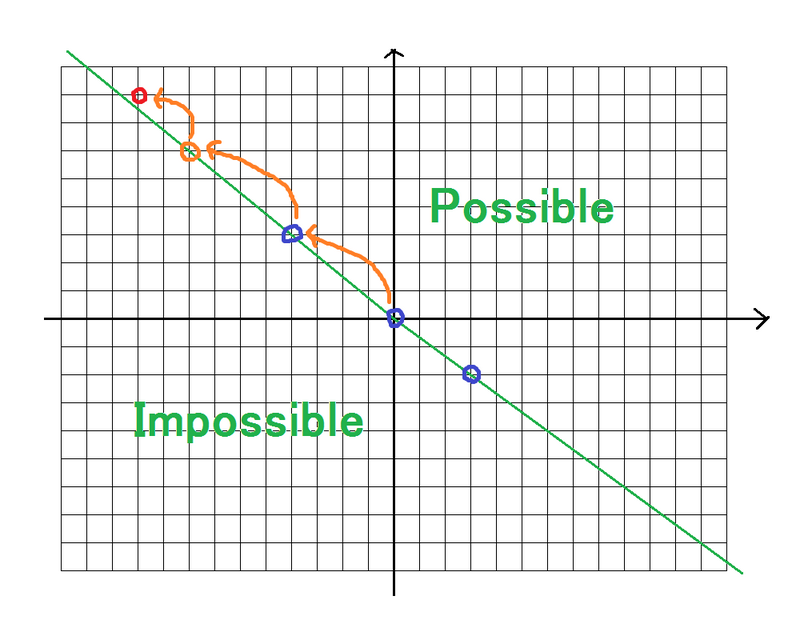
Let’s return to the original problem. For a given \(T\), does there exist a following representation?
\(T = 2 z_q - z_p +2 \{ \sum_{i=0}^{q-1} c_i (z_{i+1} - z_i) \} + r + s \sqrt{2}\)
A slow solution is as follows. Let’s try all possibities for \(z_p, z_q\) and fix them. Then, if the coordinates of \(T - (2 z_q - z_p)\) are not even, use the \(r + s \sqrt{2}\) part to fix that. After that we just check if the remaining value is within the possible region described above.
To make it faster, notice that the “possible region” depends on \(z_q\), but it doesn’t change very often. Let’s see how the region changes as \(z_q\) increases. It changes only when we update the maximum slope, and that happens only \(O(\log MAX)\) times: when \(z_q = -1 + \sqrt{2}, 2 - \sqrt{2}, 3 - 2 \sqrt{2}, \cdots\), or in terms of coordinates, \((-1, 1), (-4, 3), (-7, 5), (-24, 17), \cdots\) on the upper-left quadrant or \((2, -1), (3, -2), (10, -7), (17, -12), (58. -41), \dots\) on the lower-right quadrant.
What are these coordinates? It corresponds to the following sequence of approximation of \(\sqrt{2}\):
- \(\frac{1}{1}, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \cdots, \frac{y}{x}, \frac{2x+y}{x+y}, \cdots\)
To give a formal proof for the extremeness of these points, it is sufficient to make sure that, for example the points \((0, 0) ,(17, -12), (58, -41)\) defines a triangle of area \(1/2\) (thus no integer point can exist below the polyline connecting these extreme points). It requires some computation, but straightforward.
Finally, we get a solution. Instead of fixing \(z_q\) and \(z_p\), let’s fix the region. There are only \(O(log MAX)\) possible regions. For a fixed region, it turns out that we only need to check two possibilities of \((z_p, z_q)\), that is,
- \(z_q\) is the minimum possible value that gives the region, and \(z_p = 0\).
- \(z_q\) is the minimum possible value that gives the region, and \(z_p\) is the closest point to the left of \(z_q\) of a different type (for example, for \(z_q = 4\), \(z_p = 2 \sqrt {2}\), because \(3\) is the same type).
Again, the formal proof of this part requires some computation, but is straightforward.
The entire solution works in \(O(log MAX)\) per query.
投稿日時:
最終更新: