一回の移動を \(K\) 歩とみなすことにします．次のような dp を考えます．

\(\mathrm{dp}[(u,v)][k]\)：頂点 \(u\) から \(v\) へ，一回の移動の中の \(k\) 歩目で移る場合を考えたとき，これが起きうるような頂点 \(v\) までの歩数の最小値

頂点 \(1\) に隣接する頂点 \(v\) に対して，\(\mathrm{dp}[(1,v)][1]=1\) と初期化できます．（あるいは仮想の頂点 \(X\) を作って \(\mathrm{dp}[(X,1)][K]=0\) としても良いです．）dp の遷移は次のようになります．

• \(k\neq K\) のとき： 頂点 \(v\) に隣接する頂点 \(w\)（ただし \(w\neq u\)）ついて，\(\mathrm{dp}[(v,w)][k+1]\leftarrow \mathrm{dp}[(u,v)][k]+1\)

• \(k=K\) のとき： 頂点 \(v\) に隣接する頂点 \(w\) について，\(\mathrm{dp}[(v,w)][1]\leftarrow \mathrm{dp}[(u,v)][k]+1\)

これは BFS で計算することができますが，このままでは TLE してしまいます．なぜなら，ある \(v\) に対して \(\mathrm{dp}[(v,w)][k+1]\leftarrow \mathrm{dp}[(u,v)][k]+1\) という遷移が起きる回数を考えると，\(v\) の次数を \(d\) としたときに， \(u,w\) がそれぞれ \(d\) 通り，\(k\) が \(K\) 通りあるため，最悪で \(\Theta(N^2K)\) 回になってしまうからです．

ここで重要な考察として，ある頂点 \(v\) に対して，\(\mathrm{dp}[(v,w)][k+1]\leftarrow \mathrm{dp}[(u,v)][k]+1\) という遷移は \(2\) つの \(u\) に対してのみ行えば十分です．言い換えると，頂点 \(v\) に \((k+1)\) 歩目で踏み入れるのは \(2\) 回まで考慮すればそれで十分です．

その理由を次の図で説明します．

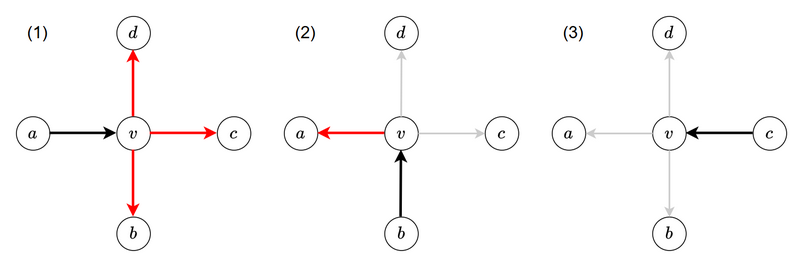
1. 初めて \(v\) に \(a\) から訪れたとき，\(v\to b, v\to c, v\to d\) の遷移が起きます．
2. 次に \(v\) に \(b\) から訪れたとき，更新される可能性があるのは \(v\to a\) のみです．\(v\to c\) や \(v\to d\) は \(1\) 回目に \(a\) から訪れたときにすでに遷移が起きています．
3. \(v\) に \(3\) 回目以降訪れたとき，\(1\) 回目と \(2\) 回目ですべて遷移は網羅しているため，新しい遷移は起きません．

よって，\(v\) に \(k\) 歩目に踏み入れたのが何回か？を持っておき， \(3\) 回目以降の処理をスキップすることで，計算量は \(O(NK)\) になります．

実装についてですが，各辺について双方向の有向辺があるとみなし，元のグラフで \(i\) 番目（0-indexed）の辺に対応する有向辺を \(2i,2i+1\) と番号付けると連想配列等を使わずに実装できます．

from collections import deque


def solve():
    N, K = map(int, input().split())
    G = [[] for i in range(N)]
    for i in range(N - 1):
        u, v = map(lambda x: int(x) - 1, input().split())
        G[u].append((v, 2 * i))
        G[v].append((u, 2 * i + 1))

    dp = [[-1] * (2 * N - 2) for i in range(K)]
    ans = [-1] * N
    cnt = [[0] * N for i in range(K)]
    dq = deque([(0, 0, -1)]) # (総歩数，頂点番号，有向辺の番号)
    while dq:
        d, v, e = dq.popleft()
        if d % K == 0 and ans[v] == -1:
            ans[v] = d // K
        if cnt[d % K][v] == 2:
            continue
        cnt[d % K][v] += 1
        for u, e2 in G[v]:
            if e ^ e2 == 1 and d % K != 0:
                continue
            if dp[(d + 1) % K][e2] == -1:
                dp[(d + 1) % K][e2] = d + 1
                dq.append((d + 1, u, e2))

    print(*ans[1:])


for _ in range(int(input())):
    solve()