 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 575 点
問題文
H 行 W 列のマス目があります。 上から i 行目 (1\le i\le H) 、左から j 行目 (1\le j\le W) のマスをマス (i,j) と呼ぶことにします。
マス目は障害物が置かれているか何も置かれていないかのいずれかで、障害物が置かれているマスはマス (r _ 1,c _ 1),(r _ 2,c _ 2),\ldots,(r _ K,c _ K) の K 個です。
高橋くんははじめマス (1,1) におり、上下左右に隣接する何も置かれていないマスに移動することを繰り返してマス (H,W) へ行きたいと思っています。
厳密には、高橋くんは以下の操作を好きなだけ繰り返すことができます。
- 次の 4 つの操作から 1 つを選び、選んだ操作を行う。
- 1\lt i かつマス (i-1,j) に何も置かれていないならマス (i-1,j) に移動する。そうでなければ移動しない。
- 1\lt j かつマス (i,j-1) に何も置かれていないならマス (i,j-1) に移動する。そうでなければ移動しない。
- i\lt H かつマス (i+1,j) に何も置かれていないならマス (i+1,j) に移動する。そうでなければ移動しない。
- j\lt W かつマス (i,j+1) に何も置かれていないならマス (i,j+1) に移動する。そうでなければ移動しない。
高橋くんがマス (1,1) からマス (H,W) へ移動できるか判定してください。
制約
- 1\le H\le2\times10 ^ 5
- 1\le W\le2\times10 ^ 5
- 0\le K\le2\times10 ^ 5
- 1\le r _ i\le H\ (1\le i\le K)
- 1\le c _ i\le W\ (1\le i\le K)
- (r _ i,c _ i)\ne(1,1)\ (1\le i\le K)
- (r _ i,c _ i)\ne(H,W)\ (1\le i\le K)
- (r _ i,c _ i)\ne(r _ j,c _ j)\ (1\le i\lt j\le K)
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
H W K r _ 1 c _ 1 r _ 2 c _ 2 \vdots r _ K c _ K
出力
高橋くんが問題文中の操作を繰り返してマス (1,1) からマス (H,W) へ移動することができるなら Yes を、そうでなければ No を出力してください。
入力例 1
4 5 5 1 4 2 3 3 2 3 4 4 2
出力例 1
No
マス目は以下のようになっています。

高橋くんはマス (1,1) からマス (4,5) まで移動することはできません。
入力例 2
2 7 3 1 2 2 4 1 6
出力例 2
Yes
マス目は以下のようになっています。
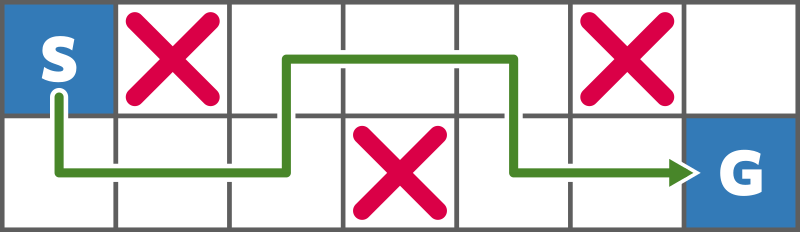
高橋くんは図のように移動することでマス (1,1) からマス (2,7) まで移動することができます。
入力例 3
1 1 0
出力例 3
Yes
高橋くんが移動しなくていい場合や、障害物がひとつも置かれていない場合があることに注意してください。
入力例 4
10 12 20 8 3 1 11 6 4 3 7 10 4 5 7 4 7 5 5 4 3 6 1 1 6 2 7 6 7 1 3 6 3 2 12 9 6 7 3 3 11 9 7
出力例 4
Yes
Score : 575 points
Problem Statement
There is an H \times W grid. Let (i,j) denote the cell at the i-th row (1\le i\le H) from the top and j-th column (1\le j\le W) from the left.
Each cell in the grid either has an obstacle placed on it or has nothing placed on it. There are K cells with obstacles: cells (r_1,c_1),(r_2,c_2),\ldots,(r_K,c_K).
Takahashi is initially at cell (1,1) and wants to reach cell (H,W) by repeatedly moving to an adjacent cell (up, down, left, right) that has nothing placed on it.
More precisely, he can repeat the following operation as many times as he likes:
- Choose one of the following four operations and perform the chosen operation:
- If 1\lt i and cell (i-1,j) has nothing placed on it, move to cell (i-1,j). Otherwise, do not move.
- If 1\lt j and cell (i,j-1) has nothing placed on it, move to cell (i,j-1). Otherwise, do not move.
- If i\lt H and cell (i+1,j) has nothing placed on it, move to cell (i+1,j). Otherwise, do not move.
- If j\lt W and cell (i,j+1) has nothing placed on it, move to cell (i,j+1). Otherwise, do not move.
Determine whether he can move from cell (1,1) to cell (H,W).
Constraints
- 1\le H\le2\times10^5
- 1\le W\le2\times10^5
- 0\le K\le2\times10^5
- 1\le r_i\le H\ (1\le i\le K)
- 1\le c_i\le W\ (1\le i\le K)
- (r_i,c_i)\ne(1,1)\ (1\le i\le K)
- (r_i,c_i)\ne(H,W)\ (1\le i\le K)
- (r_i,c_i)\ne(r_j,c_j)\ (1\le i\lt j\le K)
- All input values are integers.
Input
The input is given from standard input in the following format:
H W K r_1 c_1 r_2 c_2 \vdots r_K c_K
Output
If Takahashi can move from cell (1,1) to cell (H,W) by repeating the operation described in the problem, print Yes; otherwise, print No.
Sample Input 1
4 5 5 1 4 2 3 3 2 3 4 4 2
Sample Output 1
No
The grid looks as follows:

Takahashi cannot move from cell (1,1) to cell (4,5).
Sample Input 2
2 7 3 1 2 2 4 1 6
Sample Output 2
Yes
The grid looks as follows:

He can move from cell (1,1) to cell (2,7) by moving as shown in the figure.
Sample Input 3
1 1 0
Sample Output 3
Yes
Note that there may be cases where he does not need to move or where no obstacles are placed.
Sample Input 4
10 12 20 8 3 1 11 6 4 3 7 10 4 5 7 4 7 5 5 4 3 6 1 1 6 2 7 6 7 1 3 6 3 2 12 9 6 7 3 3 11 9 7
Sample Output 4
Yes