問題

背景

うなぎ王国の隣国うさぎ王国の前国王は，道路に関所を作るのが大好きだった．王国の至る所に，通るたびに 1 ウサドル（ウサドルはうさぎ王国の通貨単位）の通行税が取られる道が残っている．

現在のうさぎ国王はこれを廃止し国民の負担を減らしたいと考えたが，前国王派の勢力は根強く，なかなか関所を取り潰すことができない．相談を受けたうなぎ王国の王様は，この問題を解決する画期的な提案を行った．前国王派の勢力の弱い関所のない道に，通るたびに 1 ウサドルの報奨金が手渡される「逆関所」を設置してしまうのだ．こうすることで通行人の収支のバランスがとれるようになり，うさぎ王国には平和が訪れた．

さて，うさぎ王国に住まう青年うさぎ Jiro は潔癖な性格であった．国王の善意に甘えて逆関所ばかりを通りお金を稼ぐような行為は，彼には考えられない．例え遠回りになっても，同じ道を何度も回ることになろうとも，Jiro はどこへ行くにも関所と逆関所による収支がトータルで ±0 になるようなルートをとることにしている．

しかし一方で，Jiro はその潔癖な性格が災いしたため，貧乏である．どこかに出かけようとする時は，いつも所持金は 0 ウサドルなのである．あなたには，そんな Jiro のための最短経路計算プログラムを書いて欲しい．

課題

0 から N-1 の番号のついた N 頂点からなる有向グラフが与えられる．このグラフの辺は正整数の長さを持ち，また，以下の3種類の文字で表されるタイプに分類される．

• '-': 「関所」．一回通るたびに所持金が 1 減る．所持金 0 の時はこのタイプの辺は通れない．
• '+': 「逆関所」．一回通るたびに所持金が必ず 1 増える．
• '=': なにもない普通の道．所持金は変化しない．

うさぎの Jiro は所持金 0 で頂点 0 を出発し，最終的に所持金 0 で頂点 N-1 に到達したい．このような経路の最短の長さを求めよ．経路中で同じ頂点や辺を何度通っても構わない．特に，最初と最後以外で頂点 0 と N-1 を通過してもよい．

配点

300

入力

入力は以下の形式で与えられる．

N
G0
...
GN-1
L0,0 ... L0,N-1
...
LN-1,0 ... LN-1,N-1

N は頂点数，G_i=G_i,0G_i,1...G_i,N−1 は長さ N の文字列で G_i,j は頂点 i から頂点 j への辺のタイプを表す． G_i,j='x' ならば頂点 i から頂点 j には辺は存在しない．L_i,j は自然数で，0 ならば頂点 i から頂点 j への辺が存在しないこと，そうでなければ頂点 i から頂点 j への辺の長さを示す．

制約

入力中の各変数は以下の制約を満たす．

• 2\leq N\leq 250
• すべての i について G_i,i='x'
• すべての i, j について G_i,j='x' ならば L_i,j=0 ，それ以外の場合 0\lt L_i,j \lt 10,000

部分点

この問題には部分点が設定されている．この問題のテストケースのうち50点分は，追加で以下の制約も満たす．

• 2 \leq N \leq 50

出力

問題の解を1行に出力せよ．条件を満たす経路が存在しない場合は -1 と出力せよ．

入力例1

5
x+x=x
xx-xx
x+x+-
xxxx-
xxxxx
0 1 0 1 0
0 0 1 0 0
0 1 0 1 1
0 0 0 0 1
0 0 0 0 0

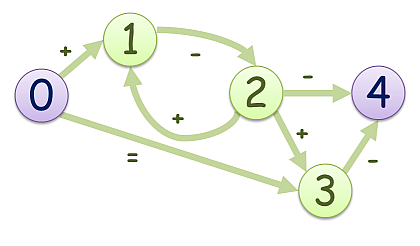
入力例1に対する出力例

4

頂点0(所持金0) → 頂点1(所持金1) → 頂点2(所持金0) → 頂点3(所持金1) → 頂点4(所持金0) という経路が解となる．これより短い経路では終点に到達したときの所持金が0にならない．

入力例2

4
x+=x
+xxx
=xx-
xx-x
0 1 1 0
1 0 0 0
1 0 0 1
0 0 1 0

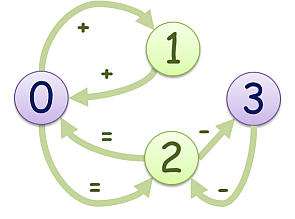
入力例2に対する出力例

-1

始点から終点への経路は存在するが，所持金がちょうど0の状態で終点に到達することはできない．

入力例3

3
x--
=x+
==x
0 58 58
42 0 58
42 42 0

入力例3に対する出力例

-1

頂点1から出る辺はすべて '-' であるため，所持金0では動くことができない．

入力例4

8
x+xxxxxx
xx+x=xxx
+xxxxxxx
xxxx-xxx
xxxxx-xx
xxxxxx-x
xxxxxxx-
xxx-xxxx
0 1 0 0 0 0 0 0
0 0 2 0 3 0 0 0
4 0 0 0 0 0 0 0
0 0 0 0 5 0 0 0
0 0 0 0 0 4 0 0
0 0 0 0 0 0 3 0
0 0 0 0 0 0 0 2
0 0 0 1 0 0 0 0

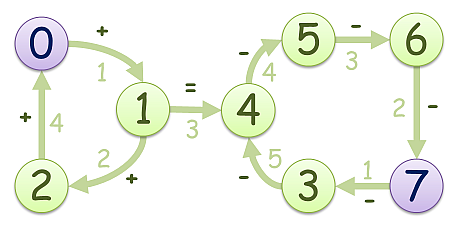
入力例4に対する出力例

71

始点や終点，またそれぞれの辺を何度も繰り返し通ってもよい．