 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題
背景
うなぎ王国にはたくさんの町があり,これらの町は支配関係にあるが,その関係は木構造になっていることが知られている.それぞれの町はどこか別の町と友好関係を結びたいと考えているが,町同士が支配関係にある場合は友好関係を結ぶことができない.またそれぞれの町はその町とできるだけ人口が近い町と友好関係を結びたいと考えている.それぞれの町がどこの町と友好関係を結べばいいのかを考えよう.
課題
各頂点が値を持つ根付き木が与えられたときに,各頂点に対してその頂点の子孫でも祖先でもない頂点の中で,その頂点の持つ値に最も近い値を持つ頂点の値を答えよ.
最も近い値を持つ頂点が複数ある場合は,その中で最も小さい値を持つ頂点の値を答えよ.またその頂点の子孫でも祖先でもない頂点が存在しない頂点に対しては -1 を出力せよ.
配点
200
入力
入力は以下の形式で与えられる.
N a1 ... aN s1 t1 ... sN-1 tN-1
N は頂点の数,ai は i 番目の頂点が持つ値,si と ti は ti が si の子供であることを表す.
制約
入力中の各変数は以下の制約を満たす.
- 1 \leq N \leq 105
- 1 \leq ai \leq 109
- 0 \leq si, ti \lt N
グラフは根付き木になっていることが保証される.
出力
出力は N 行からなる. i(1 \leq i \leq N) 行目には i 番目の頂点の子孫でも祖先でもない頂点の中で,その頂点の持つ値に最も近い値を持つ頂点の値を出力せよ.ただしその頂点の子孫でも祖先でもない頂点が存在しない頂点に対しては -1 を出力せよ.
入力例1
7 1 2 3 4 5 6 7 0 1 1 2 1 3 0 4 4 5 4 6
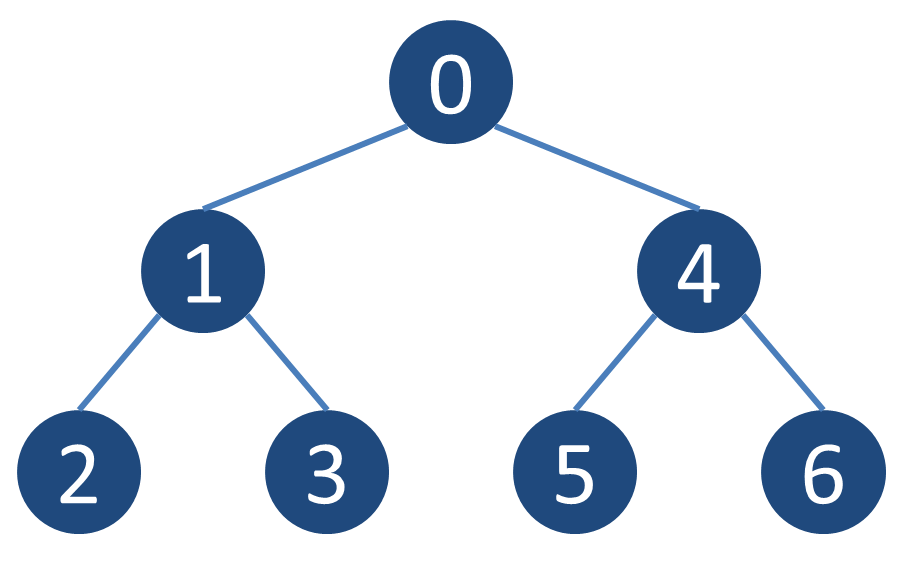
入力例1に対する出力例
-1 5 4 3 4 7 6
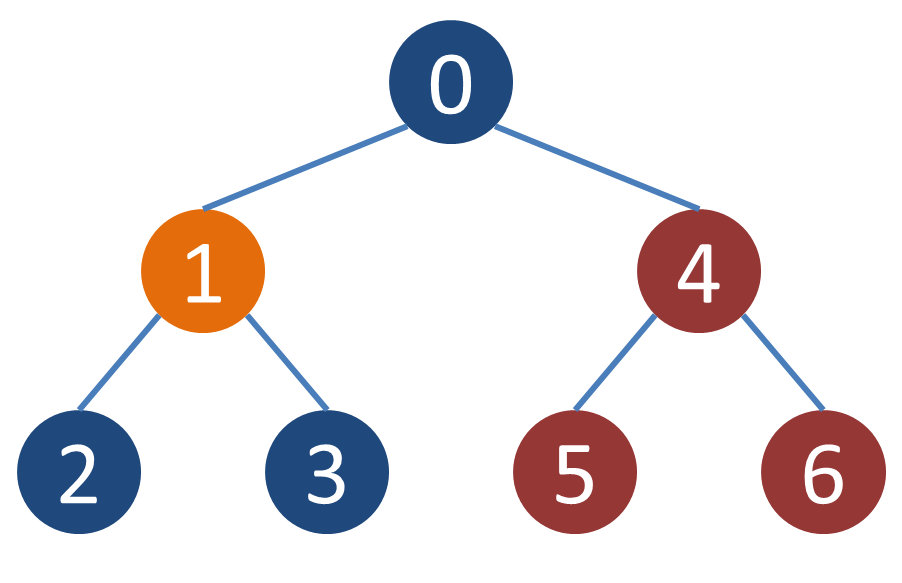
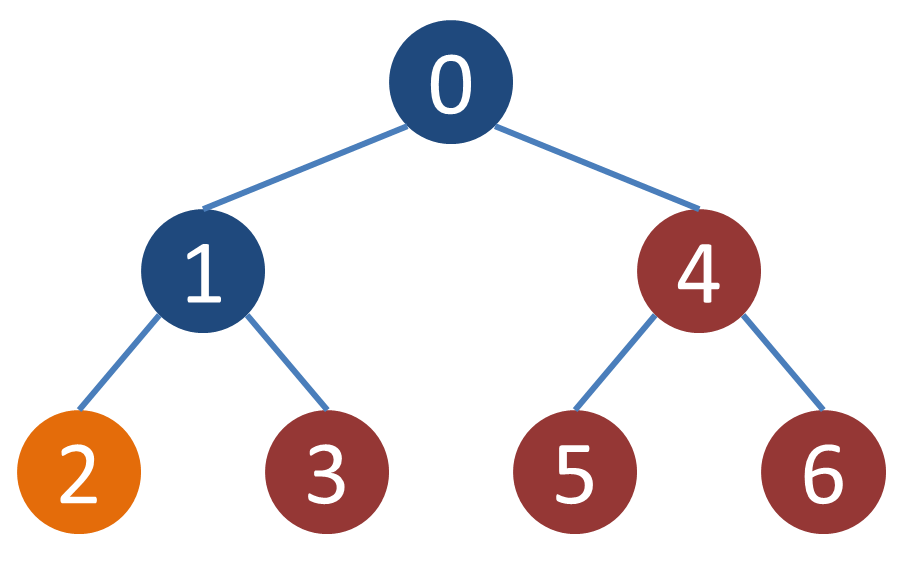
各頂点の子孫でも祖先でもない頂点がどのようになるかの一例を示す.例えば頂点1の子孫でも祖先でもない頂点は4,5,6であり,頂点2の子孫でも祖先でもない頂点は3,4,5,6のようになる.
入力例2
4 1 2 3 4 0 1 1 2 2 3
入力例2に対する出力例
-1 -1 -1 -1
すべての頂点にその頂点の子孫でも祖先でもない頂点が存在しない.
入力例3
5 1 1 2 3 4 0 1 0 2 0 3 0 4
入力例3に対する出力例
-1 2 1 2 3