問題

背景

うなぎ王国のお姫様は，データ構造が大好きだ．そこで王様は，お姫様の誕生日に「バイナリヒープを表現した配列」をたくさんプレゼントしようと準備していた．

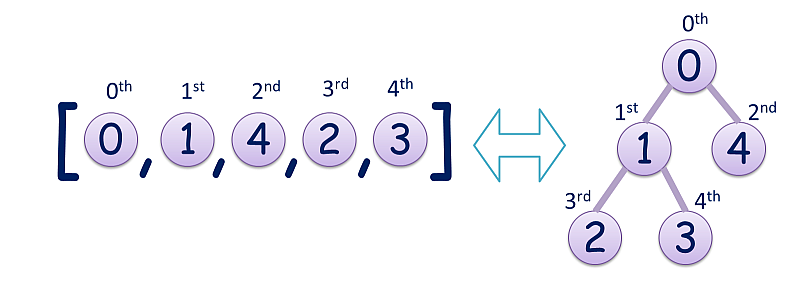
「バイナリヒープを表現した配列」とは，配列の第 i 要素の値は，第2i+1要素が存在すればそれより真に小さく，同様に第2i+2要素が存在すればそれよりも真に小さい，という条件を全ての要素で満たす配列のことを言う．たとえば [0,1,4,2,3] はバイナリヒープを表現した配列である．なぜならば，第0要素である0は第1要素と第2要素である1と4よりも小さく，第1要素である1は第3要素と第4要素の2と3よりも小さい…，という条件がすべて成り立っている．このような配列は，第i要素の子が第2i+1要素と第2i+2要素であるようなツリー構造と考えると，親の方が常に値が小さいという特徴を持つ．お姫様は，この特徴を活用してソートなど様々なアルゴリズムの効率化をするのにご執心なのだ．

さて，ところが不運なことに，王様はせっかく作った「バイナリヒープを表現した配列」を落として壊してしまった！今や王様の手元には，「バイナリヒープを表現した配列」の後半部分しか手元に残っていない．一刻も早く元の「バイナリヒープを表現した配列」を復元しなくてはならない．王様は，元の配列の要素はすべて非負整数で，重複する値はなかったことを覚えている．この情報を手がかりに配列を復元して欲しい．

課題

すなわち，入力 A₀ ... A_N-1 に対し，次を満たす配列 H₀ ... H_M-1 を求め，その長さ M を答えとして出力して欲しい．

• H_i は全て 0 以上の整数
• 配列の要素は全て互いに異なる．つまり，i \neq j ならば H_i \neq H_j
• バイナリヒープを表現した配列となっている．つまり，常に H_i \lt H_2i+1 かつ H_i \lt H_2i+2
• A が H の接尾辞となっている．つまり，全ての 0 \leq k \lt N に対し，A_k = H_M-N+k

複数の可能性がある場合は最小の M を答えること．条件を満たす H が存在しない場合は -1 と答えること．

配点

100

入力

入力は以下の形式で与えられる．

N
A0 A1 ... AN-1

制約

入力中の各変数は以下の制約を満たす．

• 1 \leq N \leq 100
• 0 \leq A_i \leq 10⁹
• A_i は互いに相異なる非負整数

出力

問題の解を1行に出力せよ．

入力例1

3
4 2 3

入力例1に対する出力例

5

[4,2,3] は，4（第0要素）が2や3（第1，第2要素）よりも大きいので，条件を満たさない．[*,4,2,3] の形の配列も，4（第1要素）が3（第3 = 2 \times 1+1要素）よりも大きいので，*にどんな値を入れても条件を満たさない．[0,1,4,2,3] が，[4,2,3] を接尾辞に持ちバイナリヒープを表現した最短の配列である．

入力例2

3
3 1 2

入力例2に対する出力例

-1

[0,1,3,1,2] や [-1,0,3,1,2] は配列の要素に重複がないこと，非負整数であることなどに反するため，条件を満たさないことに注意せよ．

入力例3

4
10 20 40 30

入力例3に対する出力例

4

入力例4

4
9 2 3 6

入力例4に対する出力例

8