問題文

頂点に 1 から n までの番号がついた n 頂点の木 t に対し、以下の条件を満たす (1, \dots, n) の順列 p = (p_1, \dots, p_n) の個数を f(t) とおきます。

• i = 1, \dots, n に対し、頂点 p_i と頂点 p_{i + 1} を結ぶ単純パスに含まれる辺が 2 本以下 (ただし、p_{n + 1} = p_1 とする)

正整数 N, K、および頂点に 1 から N までの番号がついた N 頂点の木 T_0 が与えられます。 T_0 の i 番目の辺は頂点 A_i と頂点 B_i を結びます。

T_0 を K 個つなげて得られる木を 良い木 と呼びます。 より形式的には、頂点に 1 から NK までの番号がついた NK 頂点の木 T が以下の条件を満たすとき、またそのときに限り T を良い木であるとします。

• 1\le i\le N - 1 かつ 0\le k\le K - 1 を満たすすべての整数の組 (i, k) に対し、頂点 (A_i + N\times k) と頂点 (B_i + N\times k) の間に辺が存在する

すべての良い木 T に対する f(T) の総和を 998244353 で割った余りを求めてください。

Q 個のテストケースが与えられるので、それぞれについて答えを求めてください。

制約

• 1\le Q\le 2\times 10 ^ 5
• 1\le N\le 2\times 10 ^ 5
• 1\le K\le 2\times 10 ^ 5
• 1\le A_i\lt B_i\le N
• 1 つの入力ファイルに含まれる N の総和は 2\times 10 ^ 5 以下
• 入力されるグラフは木
• 入力はすべて整数

入力例 1

5
4 1
1 2
1 3
1 4
4 1
1 2
2 3
3 4
1 4
4 2
1 2
1 3
1 4
6 200000
1 3
2 3
3 4
4 5
4 6

出力例 1

24
8
192
2304
210217795

1 つ目のテストケースについて、どの単純パスも 2 本以下の辺しか含まないため、ありうる順列が全て数えられます。

2 つ目のテストケースについて、数える順列は (1, 2, 4, 3), (1, 3, 4, 2), (2, 1, 3, 4), (2, 4, 3, 1), (3, 1, 2, 4), (3, 4, 2, 1), (4, 2, 1, 3), (4, 3, 1, 2) の 8 通りです。

3 つ目のテストケースについて、すべての 4 頂点の木 T に対する f(T) の総和を求める必要があります。 T_0 が辺を持たない場合があることに注意してください。

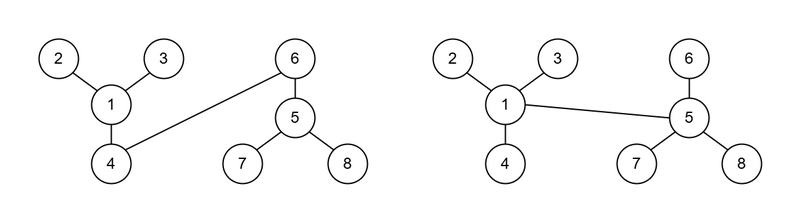
4 つ目のテストケースについて、良い木として例えば以下のような木が挙げられます。