まず \(H,W\) がともに \(4\) の倍数であることが、タイルを敷き詰める方法（以下、タイリングと呼ぶ）が存在するための必要十分条件となります。以下、 \(H,W\) はともに \(4\) の倍数であるものとします。

なお、この解説で用いられるタイリングに関する事実の証明はすべて次の \(2\) つの論文に示されています。ここではそれらの事実を認め、タイリングの性質や具体的な計算方法に焦点を当てて解説します。

• D.W. Walkup, Coveringa rectangle with T-tetrominoes, Amer. Math. Monthly 72 (1965) 986–988
• M. Korn and I. Pak, Tilings of rectangles with T-tetrominoes, Theor. Comp. Sci. 319 (2004), 3–27
  • 特に 3. Tiling rectangles with T-tetrominoes と 4. Chain graphs

タイリングの性質

\(H=W=8\) の場合のタイリングの例を示します。

実はタイルは次のような位置関係にあることはありません。

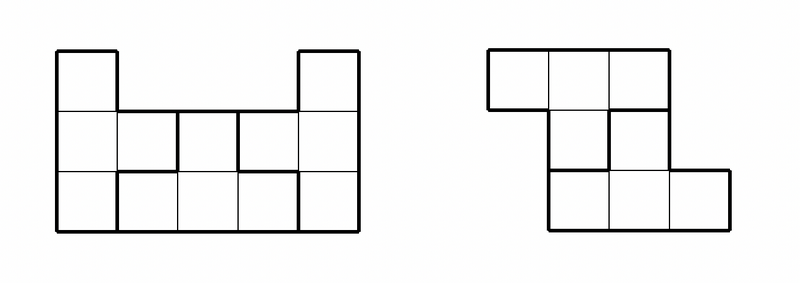
また、凹凸を噛み合わせるようにしてできるタイルは列を成しており、さらにそれはサイクルになっています。そして、タイルたちはいくつかのサイクルを成していることが確認できます。

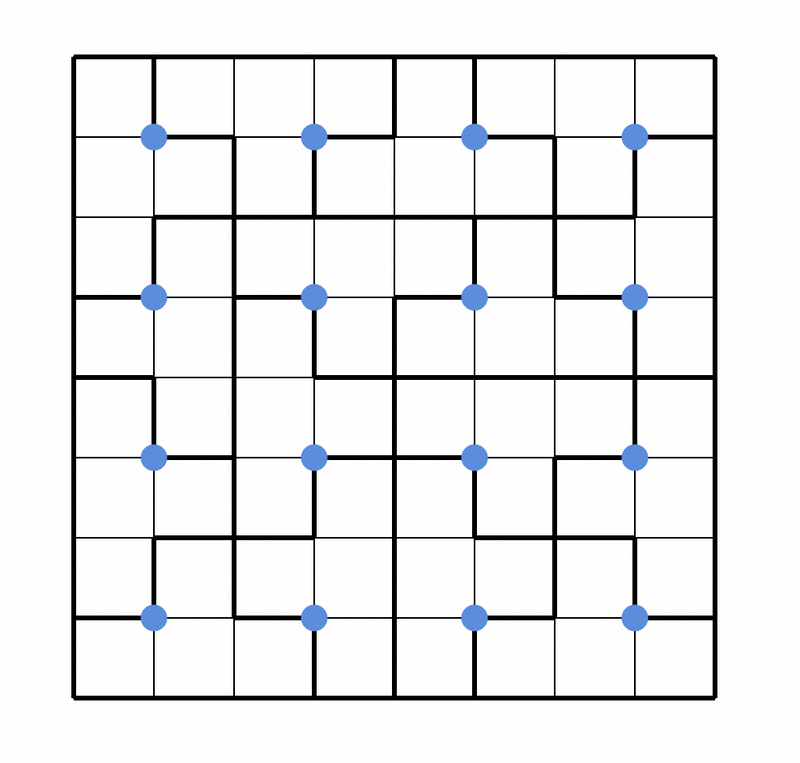
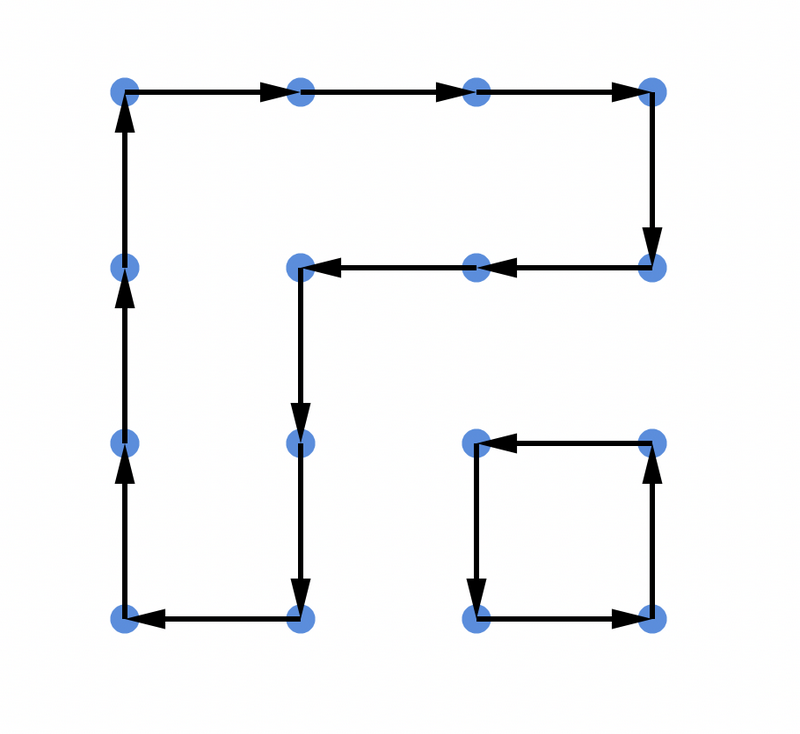
ここで、マス目の上から \(i\) 行目、左から \(j\) 列目のマスを \((i,j)\) と呼ぶことにし、 \(i,j\) が共に奇数であるようなマスの右下の角（図の青い点）に注目します。

青い点の周囲 \(4\) マスは、ある \(3\) マスが同じタイルによって覆われ、残りの \(1\) マスは別のタイルによって覆われています。同様に、タイルが覆う \(4\) マスは、ある \(3\) マスが同じ青い点の周囲 \(4\) マスに含まれ、残りの \(1\) マスは別の青い点の周囲 \(4\) マスに含まれています。そこで、青い点 \(u\) について、 \(u\) の周囲 \(4\) マスのうちちょうど \(1\) マスを覆うタイルを \(t\) とし、 \(t\) が覆うマスのうち \(3\) マスを周囲に含む青い点を \(v\) とするとき、有向辺 \(u\rightarrow v\) を考えます。この \(v\) は任意の青い点 \(u\) に対して一意に定まります。また、このようにして作られた有向グラフは、各頂点の入次数および出次数が \(1\) であり、いくつかの有向サイクルの集合になっています。こうして得られるグラフをタイリングの鎖グラフと呼ぶことにします。どのようなタイリングに対してもこのようなグラフを考えることができ、明らかにタイリングから鎖グラフを得る写像は単射です。

鎖グラフの性質

鎖グラフの特徴を整理しましょう。まず、どの辺の長さも \(2\) マス分です。さらに、グラフはいくつかのサイクルの集合になっており、各サイクルに注目すれば、次の条件が満たされています。

• 同じ方向への方向転換は奇数回辺を辿ったときにのみ起こり得る
• 違う方向への方向転換は偶数回辺を辿ったときにのみ起こり得る

そして、この性質を満たす鎖グラフはいずれも、それを与えるタイリングが存在します。さて、鎖グラフのサイクルを \(1\) つ選んで、その向きをに逆にしたものも鎖グラフです。したがって、鎖グラフに対してサイクルの個数を \(c\) として \(2^c\) の重みをつけたときの、向きを適当に固定した鎖グラフの重み付き個数を数えれば良いことになります。

ここまでの考察で、タイリングを数える問題から鎖グラフを数える問題に帰着されました。辺の向きを適当に固定し、次のグラフ上で辺をいくつか選んですべての頂点の入次数および出次数を \(1\) にする方法の個数を数え上げれば良いです。（この向き付けは方向転換の制約を反映したものになっています）

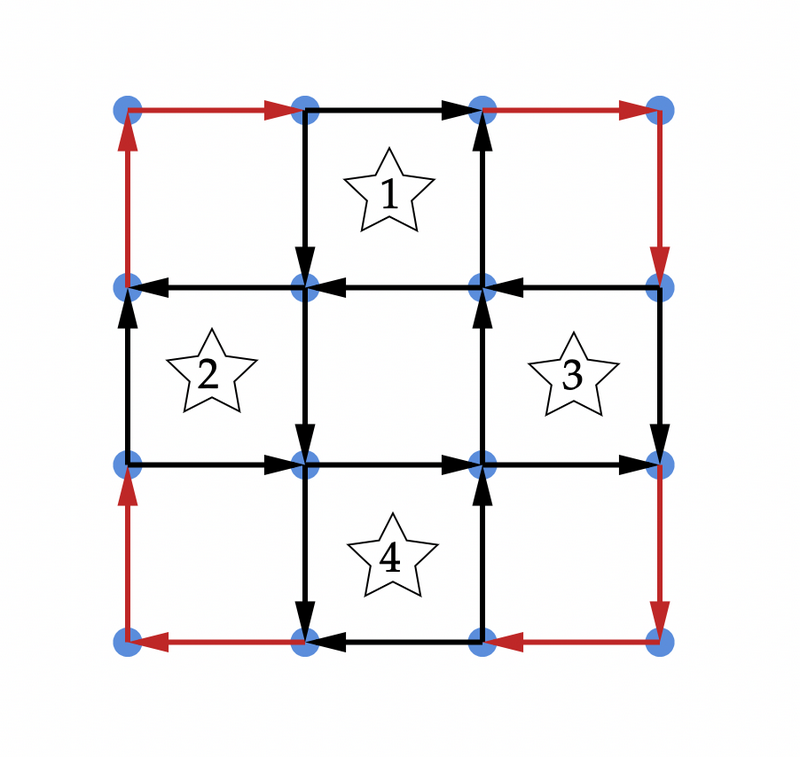
ここまでで \(H\times W\) のマス目での考察から \(H/2\times W/2\) 個の頂点での考察へとスケールが小さくなっていることに注意してください。

このグラフには、次数の条件から必ず選ばれる辺（図の赤い辺）が存在し、そうでない辺については選択肢が次のように定まっていると解釈できます。

• 印のついた部分の左右の \(2\) 辺あるいは上下の \(2\) 辺のいずれかをそれぞれ独立に選ぶことができる

たとえば、はじめに挙げたタイリングには、印 \(1,3\) は上下を、印 \(2,4\) は左右を選んだものが対応します。

数え上げ

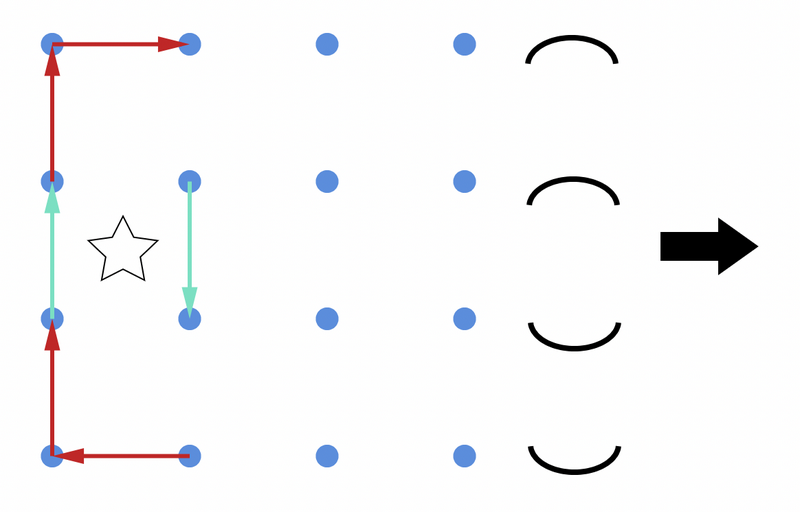
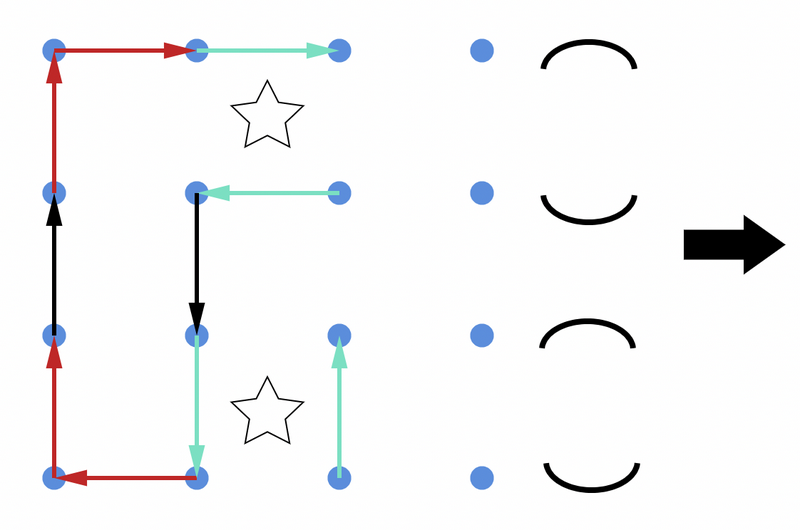
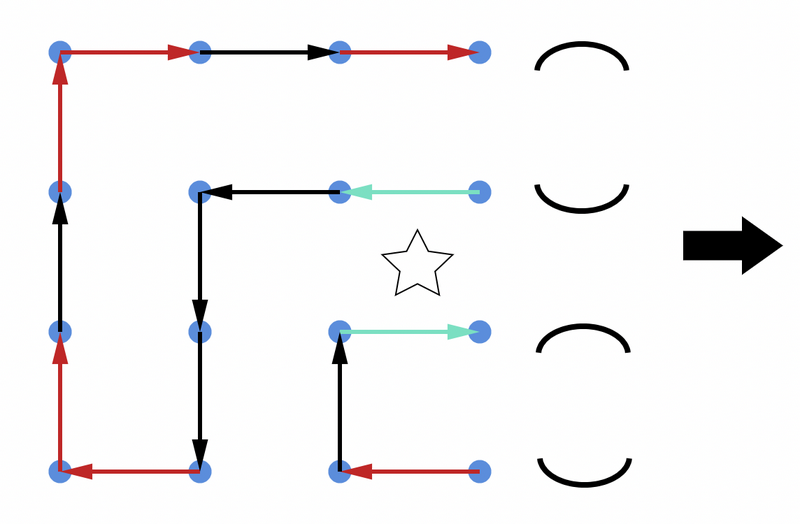
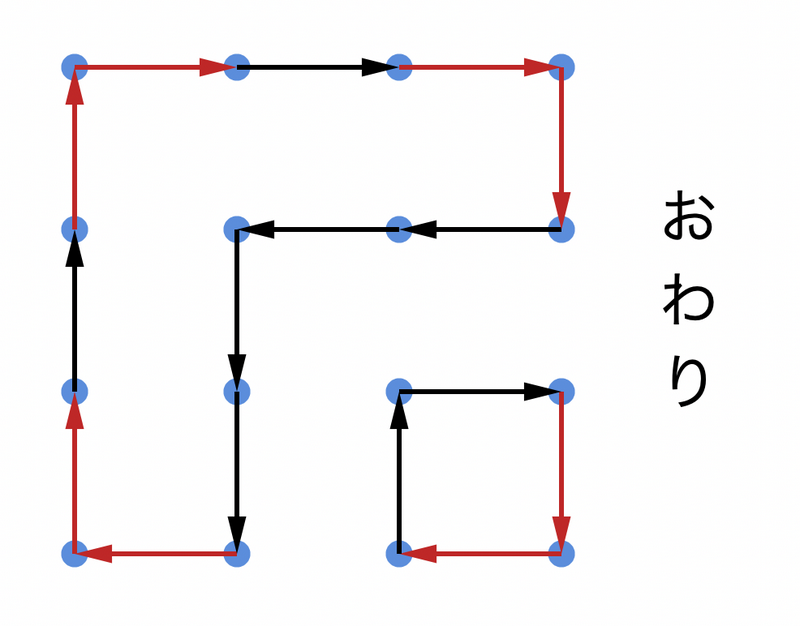
このようなグラフの数え上げには動的計画法が有効です。図のように、左から右に印を見てグラフの辺を順に選んでいくことを考えます。サイクルを \(1\) つ作るたびに重みが \(2\) 倍になることから、どのように辺を選んだらいくつのサイクルができるのかを管理する必要があります。各列の印について選択した直後、どの点がどの点と同じサイクルに属すことになるかを管理すればよく、状態数はカタラン数 \(C_n=\dfrac{(2n)!}{n!(n+1)!}\) を用いて \(C_{H/4}\) と表せます。図には各状態に対応する括弧列を横に記しています。以下、状態数を \(C\) とおきます。

この動的計画法の遷移は（列の偶奇によって処理が異なるため \(2\) 列の遷移をまとめて行えば）添字に依存しないため、素直な行列累乗で表わせる形になります。このことから列数に対する答えの列は高々 \(C\) 階の線形漸化式を持つことになります。この性質から、行列累乗を用いた \(\Theta(C^3\log W)\) で動作する解法よりも高速な解法を用いることができます。

まず初項 \(2C\) 項を行列積によって \(\Theta(C^3)\) 時間で計算した後、Berlekamp–Massey algorithm によって \(O(C^2)\) 時間で線形漸化式を復元し、Bostan-Mori algorithm によって \(O(C\log C\log W)\) 時間で最終的な答えを得ることができます。行列累乗による解法では \(C\) 次正方行列どうしの行列積を \(2\log_2 W\) 回程度計算することになり実行時間制限に間に合わないと思われますが、こちらの解法では \(C\) 次ベクトルと \(C\) 次正方行列の行列積を \(2C\) 回計算するため、ボトルネック部分から \(\Theta(\log W)\) ぶんの計算量が削減されていることに注意してください。

なお、Bostan-Mori algorithm で用いる \(2\) つの多項式を \(H=4,8,\dots, 28\) についてそれぞれ埋め込んでおけば、実行時間をより短くすることができます。

実装例(C++)