部分点(20点) 解法

\(N = 3\) の場合を考えてみましょう。このとき、自由度は「頂点 \(1,2\) の間に辺を何本張るか」「頂点 \(1,3\) の間に辺を何本張るか」「頂点 \(2,3\) の間に辺を何本張るか」の \(3\) つしかありません。それぞれを \(a,b,c\) とおくと全域木の個数 \(K\) は \(ab+bc+ca\) となります。

\(K + a^2 = (a+b)(a+c)\) と式変形することにより、

• \(K + a^2 = xy\)
• \(a \le x,y\)
• \(x + y - a \le 100 \ 000\)

をみたす \(a,\ x( := a+b),\ y( := a+c)\) を探す問題とすることができます。実は、条件を満たす \(x,y\) が存在するような \(a\) は \(0\) から \(61\) までを探すことによって必ず見つけることができます。従ってそのような \(a\) について \(K+a^2\) の約数をすべて調べることで \(x,y\) を得ることができます。

部分点(60点) 解法

次に \(N=4\) の場合を考えてみましょう。この場合張る辺の個数の自由度が \(6\) あり、それらを全探索するのは現実的ではありません。そこで行列木定理を用います。行列木定理とは、グラフのラプラシアン行列の任意の余因子がそのグラフの全域木の個数に等しいことを主張する定理です。

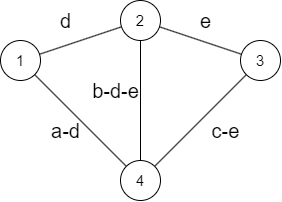
上図のグラフにおけるラプラシアン行列は

\[ \left( \begin{matrix} a & -d & 0 & -a+d \\ -d & b & -e & -b+d+e\\ 0 & -e & c & -c+e \\ -a+d & -b+d+e & -c+e & a+b+c-2d-2e \\ \end{matrix} \right) \]

でありその \((4,4)\) 余因子、すなわちこのグラフの全域木の個数は

\[ \det \left( \begin{matrix} a & -d & 0 \\ -d & b & -e \\ 0 & -e & c \\ \end{matrix} \right) = abc - ae^2 - cd^2\]

です。またこのグラフの辺の個数は \(a+b+c-d-e\) であるので、この問題は

• \(K = abc - ae^2 - cd^2\)
• \(a \ge d \ge 0\)
• \(b \ge d+e\)
• \(c \ge e \ge 0\)
• \(a+b+c-d-e \le 10000\)

を満たす \(a,b,c,d,e\) を探す問題とすることができます。

これら \(5\) つの変数を全探索するのは難しいですが、\(abc \simeq K ,\ ae^2,cd^2 \simeq 0\) を満たすように、すなわち \(a,b,c \simeq K^{\frac{1}{3}},\ d,e \simeq 0\) の周辺(具体的には \(\max(0,K^\frac{1}{3}-40) \le a,b,c \le K^\frac{1}{3}+40, 0 \le d,e \le 100\) )を探索することで条件を満たす \(a,b,c,d,e\) を高速に見つけることができます。

満点解法

\(N=5\) の場合を考えてみましょう。

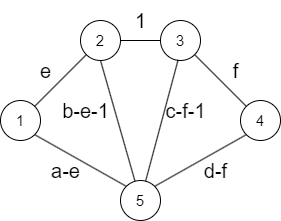
このようなグラフのラプラシアン行列の \((5,5)\) 余因子は

\[ \det \left( \begin{matrix} a & -e & 0 & 0 \\ -e & b & -1 & 0\\ 0 & -1 & c & -f \\ 0 & 0 & -f & d \\ \end{matrix} \right) \]

であり、すなわち全域木の個数は \((ab-e^2)(cd-f^2)-ad\)　、辺の数は \(a+b+c+d-e-f-1\) です。従って、

• \(K+ad = (ab-e^2)(cd-f^2)\)
• \(a \ge e \ge 0\)
• \(b \ge e+1\)
• \(d \ge f \ge 0\)
• \(c \ge f+1\)
• \(a+b+c+d-e-f \le 1001\)

を満たす \(a,b,c,d,e,f\) を探す問題とすることができます。

\(a,b,c,d = K^{\frac{1}{4}} \pm 40\) の範囲を探すことによって、条件を満たす \(e,f\) を必ず見つけることができます。また、\(x \simeq K^{\frac{1}{4}}, P \simeq K^{\frac{1}{2}}\) に対し \(xy-z^2 = P\) を満たす \(y,z\) の組を前計算しておくと、\(a,d \simeq K^{\frac{1}{4}}\) に対し \(K+ad\) の約数 \(P\) を探すことで条件を満たす \(b,c,e,f\) を高速に探すことができます。