E - 無限グラフ
解説
 /
/ 
 /
/ 
実行時間制限: 2 sec / メモリ制限: 256 MB
配点 : 1400 点
問題文
天下一研究所は、組合せ数学の研究拠点として様々な活動を行っています。 最近は、無限個の頂点を持つグラフに関する研究が盛んなようです。
正の整数 N と、0 以上 N-1 以下の整数のペア M 組 (A_1, B_1), (A_2, B_2), …, (A_M, B_M) が与えられます。
次のような、無限個の頂点を持つ無向グラフを考えます。
- 任意の整数 z に対し(負の整数も考える)、それに対応する頂点がただ一つ存在する。整数 z に対応する頂点を頂点 z と呼ぶ。どの整数にも対応しない頂点は存在しない。
- 任意の二つの整数 i, k (1 ≦ i ≦ M) に対し、頂点 A_i + k × N と頂点 B_i + (k + 1) × N は一本の辺で直接結ばれる。それらの辺以外に辺は存在しない。
(入力例・出力例のセクションの画像を参考にしてください)
このグラフの連結成分の個数が有限かどうかを判定し、有限ならその個数を求めてください。
制約
- 1 ≦ N ≦ 10^5
- 1 ≦ M ≦ 10^5
- 0 ≦ A_i, B_i ≦ N-1
- すべての組 (A_i, B_i) は異なる。
部分点
- 400 点分のデータセットは以下を満たす。
- 1 ≦ N ≦ 1000
- 1 ≦ M ≦ 1000
入力
入力は以下の形式で標準入力から与えられる。
N M A_1 B_1 A_2 B_2 : A_M B_M
出力
与えられたグラフの連結成分の個数が有限なら、その個数を出力せよ。無限なら、代わりに -1 と出力せよ。
入力例 1
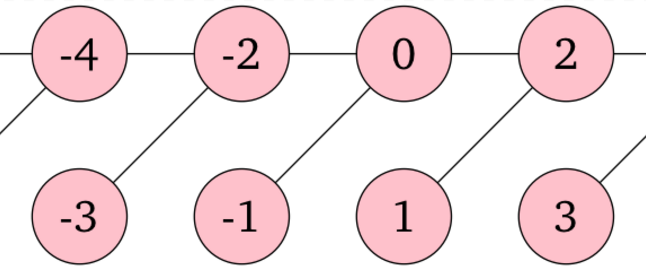
2 2 0 0 1 0
出力例 1
1

辺をたどって、任意の二頂点間を行き来できます。したがって、このグラフの連結成分の個数は 1 です。
入力例 2
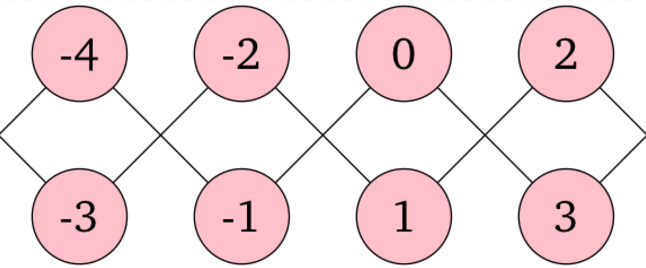
2 2 0 1 1 0
出力例 2
2

無限の長さを持つ直線状の連結成分が 2 個あります。
入力例 3
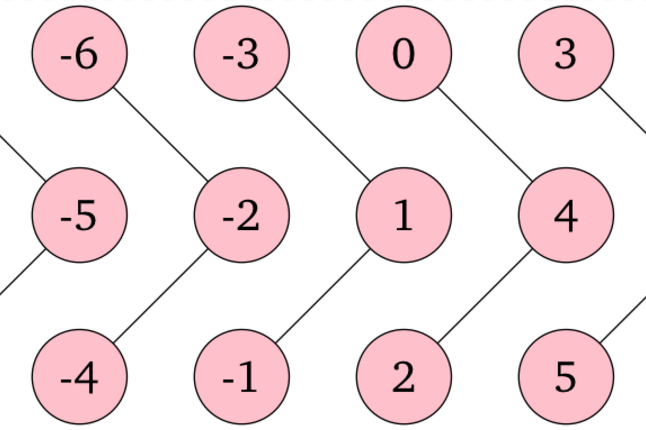
3 2 0 1 2 1
出力例 3
-1

3 頂点からなる連結成分が無限個あります。
入力例 4
7 8 0 3 1 2 1 5 2 5 3 4 4 6 5 2 6 3
出力例 4
4