スプリンクラーの円が庭を完全に包むとき、すなわち \(\sqrt{H^2+W^2}\leq 2D\) のとき、答えは \(1\) です。そうでないときを考えます。

円の面積から、庭の外に上下左右にはみ出た面積を引くことを考えます。

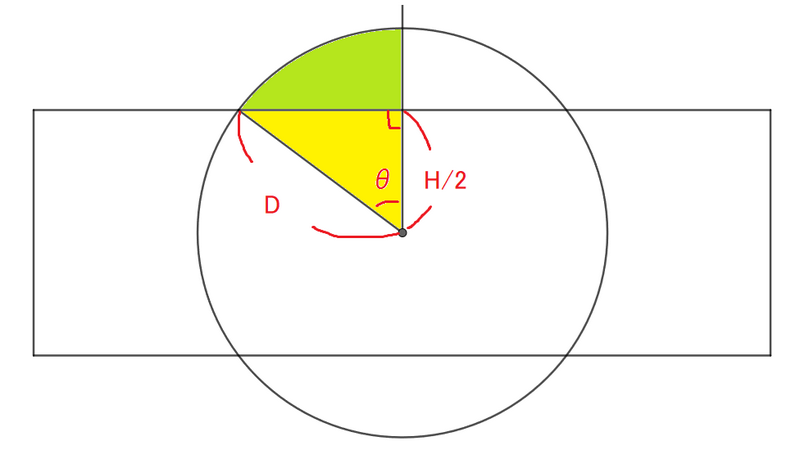
円の上にはみ出る面積は、\(2D\leq H\) のとき \(0\) です。そうでないとき、下図の緑の部分の面積の \(2\) 倍です。
緑の部分の面積は、緑と黄色をあわせた扇形の面積から、黄色の三角形を引くことで求めることができます。図の \(\theta\) で表した角度は \(\arccos\frac{H/2}{D}\) となることを用いると、扇形の面積は \(\frac{1}{2}D^2\theta\)、三角形の面積は \(\frac{1}{2}D^2\sin\theta\cos\theta\) とそれぞれ求めることができます。

左右にはみ出すケースも同様に求めることができます。

実装例(Python)

import math

def f(H,W,D):
  if H*H+W*W<=4*D*D:
    return 1
  area=D*D*math.pi
  # beyond upper/lower boundaries
  if H/2<=D:
    th=math.acos(H/2/D)
    area-=(1/2*D*D*th-1/2*D*D*math.sin(th)*math.cos(th))*4
  # beyond left/right boundaries
  if W/2<=D:
    tw=math.acos(W/2/D)
    area-=(1/2*D*D*tw-1/2*D*D*math.sin(tw)*math.cos(tw))*4
  return area/(H*W)

H,W,D=map(int,input().split())
print("{:.10f}".format(f(H,W,D)))