スライドで書いた証明がひどすぎる（というか証明になってない）のでまともな証明です。

まず、\(\text{tri}\) は言い換えると、\(3\) 点を含む極小な長方形の周長と等しいです。以降はこれを考えます。

まずは、以下を証明しましょう。

• 赤と緑の点が選ばれているとき、青い点のうち選ぶべき点は以下のどれかである \(\cdots(\spadesuit)\)
  1. x座標が最大
  2. x座標が最小
  3. y座標が最大
  4. y座標が最小
  5. x座標+y座標が最大
  6. x座標+y座標が最小
  7. x座標-y座標が最大
  8. x座標-y座標が最小

赤い点と緑の点の位置によって、領域を以下のように分けましょう。(境界上の点はどの領域に属しても良いものとします)

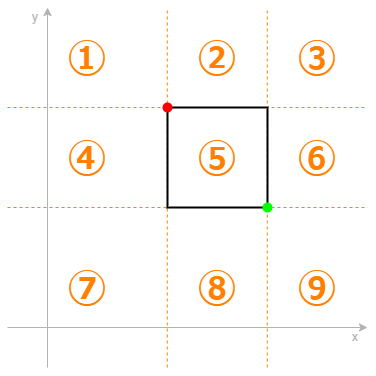
選んだ青い点が選ぶべき点に含まれていないとき、選ぶべき点のどれかに変えても悪化しないことを示します。

青い点が②、③、⑤に含まれている場合のみ証明すれば対称性よりすべて示せるので、これらを示せばよいです。

青い点が⑤に含まれている場合

このとき、青い点をどれに変えても長方形の大きさは同じになるか大きくなるので悪化しません。特に、選ぶべき点に変えても悪化しません。よって示されました。

青い点が②に含まれている場合

このとき、y座標がいまの点以上の点に変えても悪化しないことが容易に示せます。特に、y座標が最大の点に変えても悪化しません。よって示されました。

青い点が③に含まれている場合

このとき、x座標+y座標が今の点以上の点に変えても悪化しないことが示せます（これは容易ではないですが②に含まれている場合とほぼ同様に示せるので省略します）。特に、x座標+y座標が最大の点に変えても悪化しません。よって示されました。

これより、\((\spadesuit)\) が示せました。

\(1\) 点が選ばれている場合はどうでしょうか。赤い点が選ばれていると仮定すると、以下のように緑、青の点ともに選ぶべき点にすることができます。

• 緑の点を適当に選ぶ。
• 青い点を適当に選ぶ。
• 先程の議論と同様にして、青い点を選ぶべき点のどれかにする。
• 同様に、緑色の点を選ぶべき点のどれかにする。

これで、選ぶべき点のみを全探索すればよいことが示せました。\(1\) 点も指定されてない場合も同様です。これ以降はスライドを参照してください。