連結成分の分類

１つの連結成分に \(N,U,P,C\) のうちのいずれかが部分グラフとして存在する場合、その連結成分にそのアルファベットが含まれると表記します。 また、１つの連結成分に２つの \(P\) が部分グラフとして存在し、それが互いに点素であるようなとき、その連結成分に \(P+P\) が含まれると表記します。 \(P+P\) が含まれるかつ \(N\) も含まれるような場合( \(P+P\) と \(N\) は点素でなくてよい)、 \(P+P/N\) が含まれると表記します。 例えば \(P+P\) を含むグラフには必ず \(N\) が含まれますが、それは表記せず必要最小限のみ表記します。

今回の問題では、 \(10\) 頂点以下の連結無向グラフを以下のように分類することができます。

• \(P+P\) が含まれる。
• \(P+C\) が含まれる。
• \(P+C/N/P\) が含まれる。
• \(C+C/N\) が含まれる。
• \(C+C\) が含まれる。
• \(P/N\) が含まれる。
• \(P/U\) が含まれる。
• \(N\) が含まれる。
• \(U\) が含まれる。
• \(P\) が含まれる。
• \(C\) が含まれる。
• 何も含まれない。

これらの包含関係は以下の図のようになります。

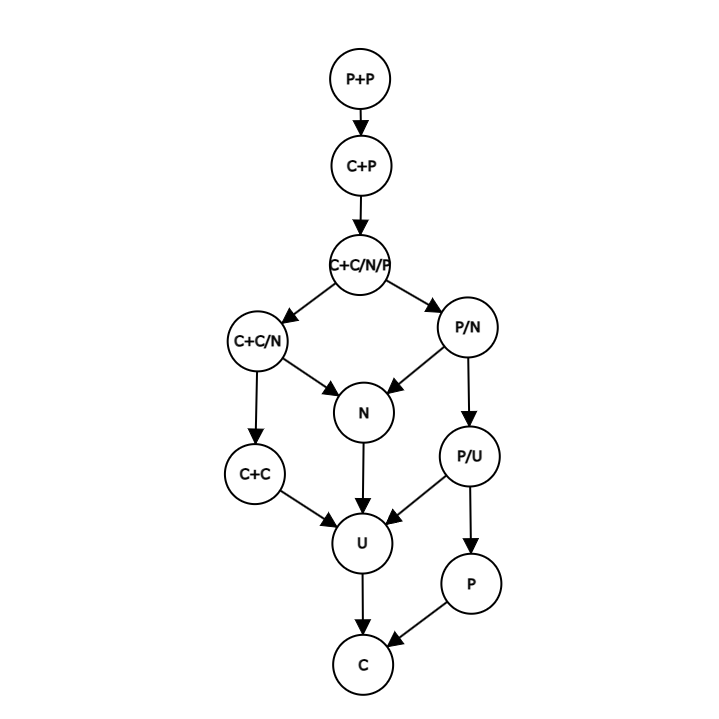
この図では矢印の根本側のノードが矢印の先端側のノードを包含していることを示しています。ここでいう包含とは、ある分類の連結成分が、包含している分類のグラフを、部分グラフとして含むことを指します。

詰め込む方法

以上のことから \(\mathrm{NUPC}\) が \(k\) 個埋め込めると仮定した時、それが可能であるかが判定できます。

まず、 \(P+P\) と \(P+C\) をそれぞれ \(P\) 2つと、 \(P\) と \(C\) に分解する数を固定します。ここではそれぞれに対して分解する数を固定するのではなく、合わせて何個分解するかを固定します。 分解する数が決まったとき、上述の包含関係から \(P+P\) を優先して分解することが最適となります。 そうすると、残っている連結成分に貪欲に文字を詰め込むことができます。 具体的には以下のように詰め込みます。

• \(P\) を \(k\) 個詰め込む

  • \(P\) が含まれるグラフに \(P\) を詰め込む。
  • \(P/U\) が含まれるグラフに \(P\) を詰め込む。
  • \(P/N\) が含まれるグラフに \(P\) を詰め込む。
  • \(C+C/N/P\) が含まれるグラフに \(P\) を詰め込む。

• \(N\) を \(k\) 個詰め込む

  • \(N\) が含まれるグラフに \(N\) を詰め込む。
  • \(P/N\) が含まれるグラフに \(N\) を詰め込む。
  • \(C+C/N\) が含まれるグラフに \(N\) を詰め込む。
  • \(C+C/N/P\) が含まれるグラフに \(N\) を詰め込む。
  • \(P+C\) が含まれるグラフに \(N\) を詰め込む。
  • \(P+P\) が含まれるグラフに \(N\) を詰め込む。

• \(U\) を \(k\) 個詰め込む

  • \(U\) が含まれるグラフに \(U\) を詰め込む。
  • \(P/U\) が含まれるグラフに \(U\) を詰め込む。
  • \(N\) が含まれるグラフに \(U\) を詰め込む。
  • \(P/N\) が含まれるグラフに \(U\) を詰め込む。
  • \(C+C\) が含まれるグラフに \(U\) を詰め込む。
  • \(C+C/N\) が含まれるグラフに \(U\) を詰め込む。
  • \(C+C/N/P\) が含まれるグラフに \(U\) を詰め込む。
  • \(P+C\) が含まれるグラフに \(U\) を詰め込む。
  • \(P+P\) が含まれるグラフに \(U\) を詰め込む。

• \(C\) を残ったグラフに \(k\) 個詰め込む

この貪欲は定数時間で動作し、 \(P+P\) と \(P+C\) に分類される連結成分は高々 \(O(N)\) 個であるため \(k\) を二分探索で決め打つことで、 \(O(N\log{N})\) 時間で最大となる \(k\) を求めることができます。

連結成分の分類方法

\(P+P, P+C, C+C\) を判定する方法

まず、頂点数が \(9\) 以下の連結成分は \(P+P, P+C, C+C\) になりません。

頂点数が \(10\) の連結成分に対しては、頂点数が \(5\) の連結成分２つに分解する方法を全探索して、それぞれに対して \(C\) や \(P\) であるかを判定すればよいです。 愚直に行うと、１つの連結成分を判定するのに計算量が \(\binom{10}{5} \times 5! = 30240\) ほどとなって、頂点数が \(10\) の連結成分が最大で \(10^4\) 個となることを考えると制限時間に間に合わせるのが難しいです。 そこで頂点数が \(5\) の連結成分には最大でも辺が \(10\) 本しか存在しないことを利用してメモ化を行うことで十分高速に判定を行うことができます。 詳しくは実装をご覧ください。

writer解

\(P, C\) を判定する方法

\(P+P, P+C, C+C\) を判定する方法と同様に、連結成分を分解する方法を全探索してメモ化を利用して判定すればよいです。

\(N, U\) を判定する方法

\(N\) は頂点数が \(7\) であるために、先ほどの方法だと高速に判定が行えません。 \(N, U\) が存在するためには、長さ \(7,6\) の単純パスが連結成分に含まれている必要があります。よって bitDP を利用して連結成分の最長単純パスを求めることで十分高速に判定を行うことができます。

クレジット

原案： nu50218

解法： nu50218, tatyam

問題準備・解説： Jinapetto

レビュー： mono_1729

テスター： physics0523

校正： nu50218