 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
あなたはロボットアームを持っています。ロボットアームの構造は、二次元平面上の折れ線 O-A-B-C で表されます(下図)。点 O は原点 (0,\ 0) に固定されています。
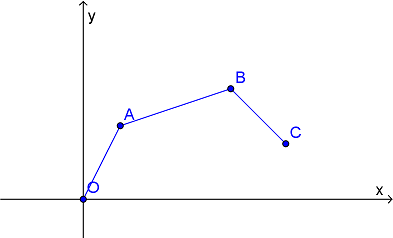
ロボットアームは、点 O,A,B で折れ線の角度を自由に変えられますが、線分 OA,AB,BC の長さは変えられません。また、折れ線には自己交差があっても構いません。
線分 OA,AB,BC の長さが与えられるので、点 C が移動できる領域の面積を求めてください。
入力
入力は以下の形式で標準入力から与えられる。
l_{OA} l_{AB} l_{BC}
- 1 行目には、線分 OA,AB,BC の長さを表す整数 l_{OA},l_{AB},l_{BC} (1≦l_{OA},\ l_{AB},\ l_{BC}≦100) が空白区切りで与えられる。
出力
点 C が移動できる領域の面積を出力せよ。絶対誤差または相対誤差が 10^{-6} 以下ならば正解となる。出力の末尾には改行を入れること。
入力例1
1 1 1
出力例1
28.2743338823
点 C が移動できる領域は、図の青い領域です。
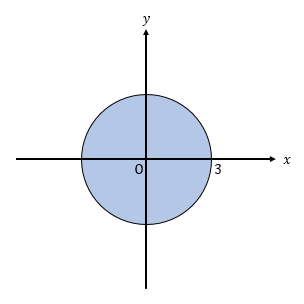
入力例2
3 1 1
出力例2
75.3982236862
点 C が移動できる領域は、図の青い領域です。
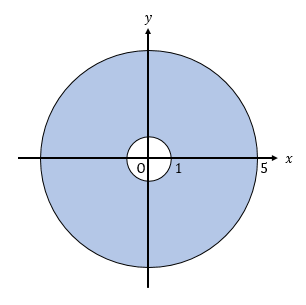
入力例3
16 2 27
出力例3
6107.2561185786
Problem
Let us think about a robot arm, which is modeled as a polyline O-A-B-C in a two-dimensional space (see the figure below). Point O is fixed at the origin, i.e., O = (0, 0).

You can modify the angles at points O, A, and B; whereas you cannot change the lengths of segments OA, AB, or BC. It is allowed for these segments to cross each other.
Given the lengths of segments OA, AB, and BC, your task is to calculate the area of the region where point C can access.
Input
The input is given from the standard input in the following format.
l_{OA} l_{AB} l_{BC}
- In the first line, you are given three integers l_{OA}, l_{AB}, and l_{BC} (1≦l_{OA},\ l_{AB},\ l_{BC}≦100), separated by spaces. They indicate the lengths of segments OA, AB, and BC, respectively.
Output
Output the area of the region where point C can access. An answer with a relative or absolute error at most 10^{-6} is considered correct. Put a newline at the end of the output.
Input Example 1
1 1 1
Output Example 1
28.2743338823
The region is illustrated in blue below.

Input Example 2
3 1 1
Output Example 2
75.3982236862
The region is illustrated in blue below.

Input Example 3
16 2 27
Output Example 3
6107.2561185786