添字を全て 0-indexed に読み替えて考えます．すなわち，問題文の \(A_{i+1},X_{i+1,j+1}\) の値を \(A_i,X_{i,j}\) で表します．

部分点 : \(M=1\)

\(M=1\) なので，長さ \(N\) の数列でちょうど一つの要素が \(1\)，他が \(0\) であるようなもののみ考えればよいです．\(0\leq k\lt N\) に対し長さ \(N\) の数列 \(E_k\) を以下のように定めます．

\[E_k=(\underbrace{0,\dots,0}_{k},1,0,\dots,0)\]

さて，\(X_{i,j}\) の様子は下図の左側のように表せます．これを右側のように拡張することを考えます．

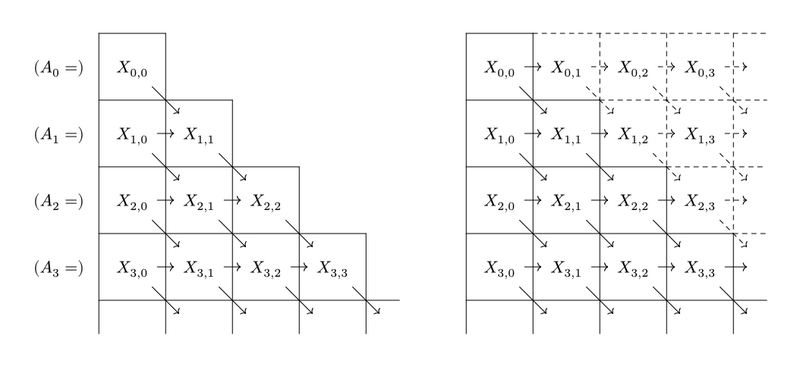
このように考えたとき，\(E_k\) についての \(\{X_{i,j}\}\) は \(E_0\) についての \(\{X_{i,j}\}\) を \(k\) マス分”下”にずらしたものになっています． 従って \(A=E_0\) のときの \(X_{i,j}\ (0\leq i,j\lt N)\) の値を愚直に \(O(N^2)\) で計算すれば，累積和や主客転倒などによってスコアの総和は \(O(N^2)\) で計算できます（部分点1）．

高速化のために \(X_{i,j}\) をもう少し具体的に考えます．

例： $A=E_2$ のときの $X_{i,j}$

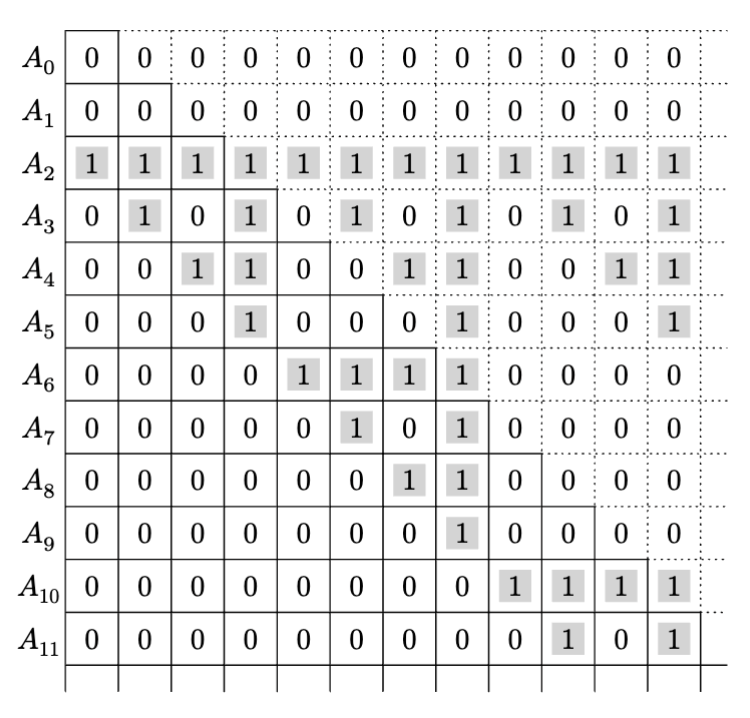
\(X_{i,j}\) はシェルピンスキーのギャスケットと呼ばれる構造（を90度回転したもの）になっており，\(A=E_k\) のとき \(X_{i,j}=\binom{j}{i-k}\bmod 2\) です． 主客転倒すれば求める値は以下のように表せます．

\[\sum_{n=0}^{N-1}(N-n)\sum_{r=0}^{n}\left(\binom{n}{r}\bmod 2\right)\]

\(s(n)=\sum_{r=0}^{n}\left(\binom{n}{r}\bmod 2\right)\) が高速に列挙できればよいです．実験すれば \(n=0\) から順に \(s(n)\) の値は以下のようになります．

\[1,2,2,4,2,4,4,8,2,4,4,8,4,8,8,16,2,\dots\]

これは以下のような特徴をもつので，再帰的に \(O(N)\) で列挙できます．

• \(s(2n)=s(n),s(2n+1)=2s(n)\)
• \(s(2^i+j)=2s(j)\ (0\leq j\lt 2^i)\)

また具体的に \(s(n)=2^{\mathrm{popcount}(n)}\) と表せます．これは上の特徴から従うほか，OEIS で調べれば載っています：A001316．

満点解法

もとの問題の答えを \(f(S)\)，数列の要素を \(0,1\) に制限したときの問題の答えを \(g(S)\) とすると，二進数表記の桁ごとに考えれば \(f(1),\dots,f(M)\) は \(g(1),\dots,g(M)\) から計算量 \(O(M\log M)\) などで求められます．

\(A\) の要素が \(0,1\) のとき，任意の \(i,j\ (0\leq j\leq i\leq N-1)\) について以下が成り立ちます．

\[ X_{i,j}=\left(\sum_{k=0}^{j}\binom{j}{k}A_{i-k}\right)\bmod{2} \]

Lucas の定理より \(\binom{j}{k}\bmod 2 = 1\) であるような \(k\) は \(2^{\mathrm{popcount}(j)}\) 個存在し，そのような \(k\) のうち奇数個について \(A_{i-k}=1\) のとき，またその時に限り \(X_{i,j}=1\) となります． よって以下が成り立ちます：

\[ g(S)=\sum_{j=0}^{N-1}(N-j)\sum_{k\text{:odd}}\binom{2^{\mathrm{popcount}(j)}}{k}\binom{N-2^{\mathrm{popcount}(j)}}{S-k}. \]

整数 \(n\ (0\leq n\leq \log_2 N)\) についての \(\mathrm{popcount}(j)=n\) となる \(j\ (0\leq j\leq N-1)\) に対する \(N-j\) の総和は dp などで計算量 \(O((\log N)^2)\) で求められます． その結果を用いれば上式より \(g(S)\) は計算量 \(O(M\log M\log N)\) で列挙できるので，この問題は全体で計算量 \(O(M\log M\log N+(\log N)^2)\) で解けます．