イクタ君の住む町にはN個の塔がある。 それぞれの塔には0からN-1までの異なる番号が与えられており、番号iの塔を塔iと呼ぶ。 好奇心旺盛なイクタ君はN個の塔の高さに興味を持ち、それらの大小関係を表す表Tを作ることにした。 TはN \times N個の要素を持ち、各要素T_{i, j} (0 \leq i, j \leq N - 1)は次のように定義される。

• T_{i, j} = -1⇔ 塔iの高さが塔jの高さより小さい

• T_{i, j} = 0 ⇔ 塔iの高さと塔jの高さが等しい

• T_{i, j} = 1 ⇔ 塔iの高さが塔jの高さより大きい

イクタ君は表Tを作成するための調査として、2つの塔を選びそれらの高さを比較するということをN-1回繰り返した。

イクタ君の調査に関して以下のことがわかっている。

• i回目の比較(1 \leq i \leq \ N - 1)で塔a_i, 塔b_iが選ばれたとすると塔a_iの高さが塔b_iの高さより大きかった。つまりT_{ai, bi} = 1, T_{bi, ai} = -1であった。

• それぞれの塔は自分自身よりも大きな塔とは高々一回しか比較されていない。

残念ながらイクタ君の調査による情報だけで表Tの内容を一意に決めることができるとは限らない。 表Tがイクタ君の調査と矛盾せず、Tが定義されるような塔の高さの組み合わせが存在するときTを正しい表と呼ぶことにする。 正しい表として何通りのものが考えられるかを計算してイクタ君に教えて欲しい。

ただし、比較された２つの塔の高さは互いに異なるがすべての塔の高さが互いに異なるとは限らない。

Input

入力は以下の形式で与えられる。

N
a₁ b₁
...
a_N-1 b_N-1

Nは塔の数を表す。 a_i, b_i (1 \leq i \leq N - 1)は塔a_iが塔b_iより高いことを表す。

Constraints

入力中の各変数は以下の制約を満たす。

• 1 \leq N \leq 200

• 0 \leq a_i, b_i < N

• a_i \neq b_i

• 異なる塔が同じ高さであることもある。

• イクタ君の調査結果自体が矛盾していることはなく、少なくとも1つイクタ君の調査結果と矛盾しない表Tが存在する。

Output

考えられる正しい表Tの個数の数を1,000,000,007で割ったあまりを出力せよ。

Sample Input 1

3
0 1
1 2

Output for the Sample Input 1

1

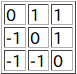
• 正しい表Tは上図の1通りである。

Sample Input 2

3 
0 1
0 2 

Output for the Sample Input 2

3

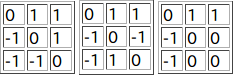
• 正しい表Tは上図の3通りである。

Sample Input 3

1 

Output for the Sample Input 3

1

• 正しい表Tは上図の1通りである。

Sample Input 4

7
0 1
1 2
2 3
3 4
0 5
0 6

Output for the Sample Input 4

91