 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1200 点
問題文
配列が N 個あります。 最初、どの配列も長さ M で、整数が (1,2,...,M) の順に並んでいます。
高橋君は、これら N 個の配列に対して、計 Q 回の操作を行うことにしました。 i (1≤i≤Q) 回目の操作では、次のような操作を行います。
- N 個の配列のうち好きなものをひとつ選ぶ。 その配列において、整数 a_i (1≤a_i≤M) を先頭へ移動する。 例えば、a_i=2 のとき、配列 (5,4,3,2,1) を選んで操作を行うと、この配列は (2,5,4,3,1) へ変わる。
高橋君の目標は、計 Q 回の操作の後、N 個の配列がまったく同じになっていることです。 計 Q 回の操作の後、N 個の配列がまったく同じになるようにできるか判定してください。
制約
- 2≤N≤10^5
- 2≤M≤10^5
- 1≤Q≤10^5
- 1≤a_i≤M
入力
入力は以下の形式で標準入力から与えられる。
N M Q a_1 a_2 ... a_Q
出力
計 Q 回の操作の後、N 個の配列がまったく同じになるようにできるならば、Yes を出力せよ。
できないならば、No を出力せよ。
入力例 1
2 2 3 2 1 2
出力例 1
Yes
例えば、図のように操作を行えばよいです。
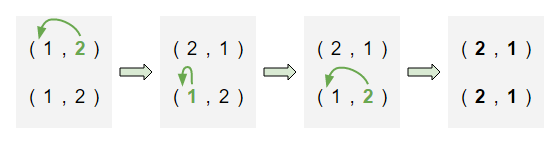
入力例 2
3 2 3 2 1 2
出力例 2
No
入力例 3
2 3 3 3 2 1
出力例 3
Yes
例えば、図のように操作を行えばよいです。
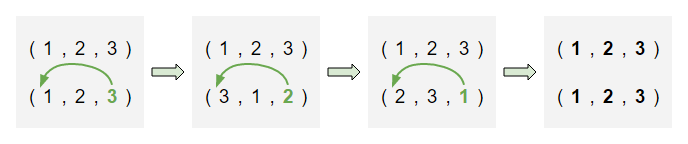
入力例 4
3 3 6 1 2 2 3 3 3
出力例 4
No
Score : 1200 points
Problem Statement
There are N arrays. The length of each array is M and initially each array contains integers (1,2,...,M) in this order.
Mr. Takahashi has decided to perform Q operations on those N arrays. For the i-th (1≤i≤Q) time, he performs the following operation.
- Choose an arbitrary array from the N arrays and move the integer a_i (1≤a_i≤M) to the front of that array. For example, after performing the operation on a_i=2 and the array (5,4,3,2,1), this array becomes (2,5,4,3,1).
Mr. Takahashi wants to make N arrays exactly the same after performing the Q operations. Determine if it is possible or not.
Constraints
- 2≤N≤10^5
- 2≤M≤10^5
- 1≤Q≤10^5
- 1≤a_i≤M
Input
The input is given from Standard Input in the following format:
N M Q a_1 a_2 ... a_Q
Output
Print Yes if it is possible to make N arrays exactly the same after performing the Q operations.
Otherwise, print No.
Sample Input 1
2 2 3 2 1 2
Sample Output 1
Yes
You can perform the operations as follows.

Sample Input 2
3 2 3 2 1 2
Sample Output 2
No
Sample Input 3
2 3 3 3 2 1
Sample Output 3
Yes
You can perform the operations as follows.

Sample Input 4
3 3 6 1 2 2 3 3 3
Sample Output 4
No