 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
10^{100} 個の白いマスが横 1 列に並んでいます。左から i (1≦i≦10^{100}) 番目のマスをマス i と呼びます。
また、駒が N 個あり、i (1≦i≦N) 番目の駒を駒 i と呼びます。
さらに、0 から 10^{100} までの数を数えることのできるカウンタが 1 つあります。
これらのマスと駒に対し N 回の操作を行います。i (1≦i≦N) 回目の操作は以下のように行います。
- まず、マス S_i に駒 i を置き、カウンタを 0 に初期化する。
- 駒のあるマスの色が白ならそのマスを黒に塗ってカウンタを 1 増加させ、駒のあるマスの色が黒なら 1 つ右のマスに駒を移動させる。
- 2. を繰り返していき、カウンタの値が C_i になったらその時点で操作を終了する。
これらの操作が終わった時点で N 個の駒がそれぞれどのマスにあるかを求めてください。
入力
入力は以下の形式で標準入力から与えられる。
N S_1 C_1 S_2 C_2 : S_N C_N
- 1 行目には、整数 N (1 ≦ N ≦ 10^5) が与えられる。
- 2 行目からの N 行には、各操作の情報が与えられる。このうち i (1 ≦ i ≦ N) 行目には、整数 S_i (1 ≦ S_i ≦ 10^9), C_i (1≦C_i≦10^9) が与えられる。これは i 回目の操作のはじめに駒 i を置くマスがマス S_i であり、カウンタが C_i になった時点で操作 i が終了となることを表す。
部分点
この問題には部分点が設定されている。
- 全ての操作が終わった時点での駒のあるマスの番号が全て 10^5 以下であるデータセットに正解した場合は、35 点が与えられる。
- N ≦ 1000 を満たすデータセットに正解した場合は、上記とは別に 40 点が与えられる。
- 追加の制約のないデータセットに正解した場合は、上記とは別に 25 点が与えられる。
出力
出力は N 行からなる。このうち i (1≦i≦N) 行目には、全ての操作が終わった時点で駒 i があるマスの番号を表す 1 つの整数を出力せよ。出力の末尾にも改行を入れること。
入力例1
4 3 3 10 1 4 2 2 4
出力例1
5 10 7 11
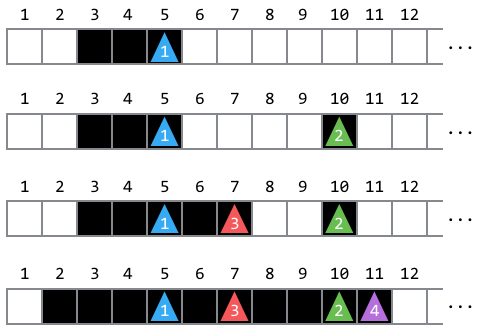
下図は各操作後のマスと駒の状態を表しています。
入力例2
8 2 1 3 1 1 1 5 1 1 1 9 1 8 2 7 9
出力例2
2 3 1 5 4 9 10 18
入力例3
5 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
出力例3
1999999999 2999999999 3999999999 4999999999 5999999999
出力が 32 bit整数型に収まらない場合もあることに注意してください。
Problem Statement
10^{100} squares are arranged in a row. The squares are numbered 1 through 10^{100} from left to right.
We have N pieces numbered 1 through N, and a counter that can store an integer between 0 and 10^{100}, inclusive.
We will perform N processes using these tools. Initially, the squares are painted white. The i^{th} (1≦i≦N) process is as follows:
- Place piece i on square S_i, and set the counter to 0.
- Look at the color of the square where piece i is placed. If the square is white, paint it black and increment the counter by 1. Otherwise (if the square is black), move piece i one square right. As a result, a square may contain multiple pieces.
- Terminate the process if the value of the counter is C_i. Otherwise, go back to step 2.
Find the final position of each of the N pieces after all the N processes.
Input
Input is given from Standard Input in the following format:
N S_1 C_1 S_2 C_2 : S_N C_N
- The first line contains an integer N (1 ≦ N ≦ 10^5).
- The following N lines describe the processes. The i^{th} (1 ≦ i ≦ N) of them contains two space-separated integers S_i (1 ≦ S_i ≦ 10^9) and C_i (1≦C_i≦10^9), denoting the initial position of piece i in the i^{th} process and the termination condition of the i^{th} process, respectively.
Partial Points
Partial points may be awarded in this problem:
- 35 points will be awarded for passing the test set satisfying the following: The number of the square where each piece is located after all the processes does not exceed 10^5.
- Another 40 points will be awarded for passing the test set satisfying N ≦ 1000.
- Another 25 points will be awarded for passing the test set without additional constraints.
Output
Print N lines, the i^{th} (1≦i≦N) of which should contain the number of the square where the piece i is located after all the N processes. Be sure to print a newline at the end of output.
Sample Input 1
4 3 3 10 1 4 2 2 4
Sample Output 1
5 10 7 11
Illustrated below is the state of the squares and the pieces after each process:

Sample Input 2
8 2 1 3 1 1 1 5 1 1 1 9 1 8 2 7 9
Sample Output 2
2 3 1 5 4 9 10 18
Sample Input 3
5 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
Sample Output 3
1999999999 2999999999 3999999999 4999999999 5999999999
Beware that the correct output may not fit into a 32-bit integer.