Hints: https://atcoder.jp/contests/arc210/editorial/14585

[1] Rephrasing cost as Manhattan distance

Take and fix one \((x_i,y_i)\) such that \(A_i=ax_i+by_i\).

Operations can be thought of as increments/decrements to \(x_i\) and \(y_i\). Since these cost \(s\) and \(t\), we have:

• The cost \(\mathrm{cost}(A_i\to B_j)\) to change \(A_i\) to \(B_j\) is the minimum possible Manhattan distance from \((sx_i,ty_i)\) to \((sz, tw)\), where \((z,w)\) ranges over those satisfying \(B_j=az+bw\).

Furthermore, by appropriate swapping, we assume \(bs\geq at\). Then, there exists an optimal solution where the number of increments/decrements to \(x_i\) is less than \(b\). This can be proved by considering replacing \(b\) “\(+a\)” operations with \(a\) “\(+b\)” operations, and so on.

With this in mind, we take \(x_i, y_i\) to satisfy \(0\leq x_i<b\). Then, the target \((z,w)\) satisfies \(-b\leq z < 2b\). There are only three such \((z,w)\) for each \(B_j\).

Organizing this situation, we have the following:

• Define point \(P_i\) in the 2D plane as follows: if \(A_i=ax+by\), \(0\leq x<b\), then \(P_i(sx,ty)\).
• Furthermore, define \(Q_j, R_j, S_j\) as follows: if \(B_j=az+bw\), \(0\leq z<b\), then \(Q_j(s(z-b),t(w+a))\), \(R_j(sz,tw)\), \(S_j(s(z+b),t(w-a))\).
• Now, \(\mathrm{cost}(A_i\to B_j)\) equals \(\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\), where \(\mathrm{dist}\) is the Manhattan distance.

[2] Computing the answer

• \(\mathrm{dist}(P_i,Q_j)=\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\)
• \(\mathrm{dist}(P_i,R_j)=\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\)
• \(\mathrm{dist}(P_i,S_j)=\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\)

The following figure illustrates on a plane the regions formed by the set of all \(P_i\) satisfying each condition:

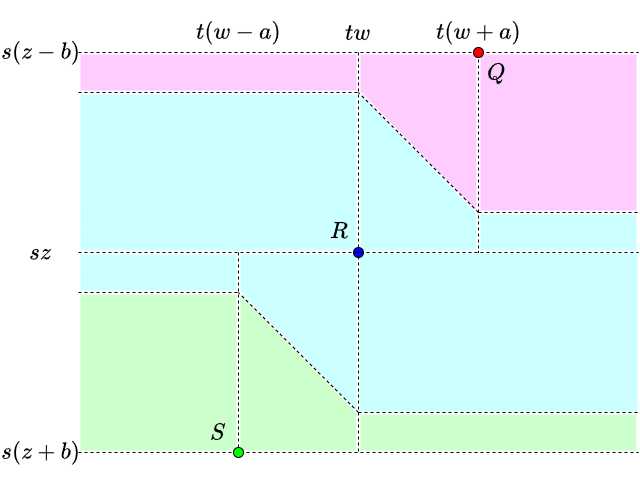
Therefore, to find the answer, we need to be able to find, for each of the \(12\) regions divided by dotted lines, the number of \(P_i\) in that region and the sum of \(x\) coordinates and \(y\) coordinates.

The rest is a basic problem about rectangular queries. For trapezoidal regions, by representing them as the difference of two regions extending infinitely in some direction as follows, we can reduce them to rectangular queries (under appropriate coordinate transformation).

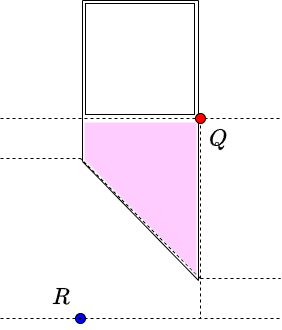
From the above, this problem can be solved in about \(O((N+Q)(\log N+\log Q))\) time. Although it is a bit tough because we need to accurately specify multiple regions, the implementation can be somewhat simplified by noting that the processing to be performed for the \([s(z-b),sz)\) part and the \([sz,s(z+b))\) part has the same form, among other things.