C - Maximize Sum of Mex Editorial
by  potato167
potato167
\(\min(B_{i}, B_{P_{i}}) = 0\) かつ \(\max(B_{i}, B_{P_{i}}) = 1\) を満たす \(i\) の数を \(X\) とし、\(\max(B_{i}, B_{P_{i}}) = 0\) を満たす \(i\) の数を \(Y\) とします。このとき、\(B\) のスコアは \(2A_{0} + X - Y\) となります。
\(A_{0}\) はクエリごとに固定であるため、上記のように定義された \(X, Y\) の \(X - Y\) の値を最大化する問題になります。
\(B\) を全て \(2\) で初期化し、\(A_{0}\) 個の要素を \(0\) に変更したあと、\(A_{1}\) 個の \(2\) である要素を \(1\) に変更して \(B\) を構築することを考えます。
このとき \(A_{1}\) の値に関わらず、\(A_{0}\) の値のみによって \(0\) に変更する箇所を決めて良いです。
\(A_{0}\) を固定し \(0\) に変更する箇所を決めたとき、\(2\) を \(1\) に変更することで \(X\) が \(2\) 増えるような箇所の数を \(C[2]_{A_{0}}\) とし、\(X\) が \(1\) 増えるような箇所の数を \(C[1]_{A_{0}}\) とし、\(\max(B_{i}, B_{P_{i}}) = 0\) の箇所の数を \(Y_{A_{0}}\) とします。
ある変更方法が他の変更方法と比べて \(Y_{A_{0}}\) が大きくないかつ \(C[2]_{A_{0}} - Y_{A_{0}}\) が小さくなければ、そのような変更方法は最適であると言えます。そして、そのような変更方法は任意の \(A_{0}\) に対して存在します。
具体的には、以下の順に \(0\) の数が \(A_{0}\) 個になるまで変更を続ければ良いです。
- 偶数サイクルに対して最大で半分のサイズだけ一個飛ばしで \(0\) に変更する。変更するサイクルの順番は任意でいいが、\(2\) のみを含むサイクルと、ちょうどサイクルの半分のサイズが \(0\) のサイクルのみにできるならそのように埋める。
- 奇数サイクルの半分のサイズ(切り捨て)だけ一個飛ばしで \(0\) に変更する。変更する順番はサイクルの大きい順。
- サイズが \(1\) でない奇数サイクルであって、\(2\) と隣り合っている \(2\) を \(1\) つ選んで \(0\) に変更する。
- サイズが \(1\) であるサイクルを選び \(0\) に変更する。
- 残っている \(2\) を任意の順に \(0\) に変更する。
例えば 1 の手順でサイズ \(6\) のサイクルを変更するときは以下のようになります。
2 - 2 - 2 - 2 - 2 - 2
2 - 0 - 2 - 2 - 2 - 2
2 - 0 - 2 - 0 - 2 - 2
2 - 0 - 2 - 0 - 2 - 0
例えば 2 の手順でサイズ \(7\) のサイクルを変更するときは以下のようになります。
2 - 2 - 2 - 2 - 2 - 2 - 2
2 - 0 - 2 - 2 - 2 - 2 - 2
2 - 0 - 2 - 0 - 2 - 2 - 2
2 - 0 - 2 - 0 - 2 - 0 - 2
\(C[2]_{A_{0}}\) と \(C[1]_{A_{0}}\) と \(Y_{A_{0}}\) が任意の \(A_{0}\) についてわかっていれば、クエリを \(O(1)\) で処理することができるので、これらの値を求めることを目標とします。
\(N\) 頂点で、\(N\) 辺の辺 \((i, P_{i})\) が存在するグラフを \(G\) とし、それぞれの連結成分のサイズを並べた列を \(S = (S_{1}, S_{2}, \dots, S_{|S|})\) とします。また、\(S\) のうち偶数であるものを並べた列を \(S_{even}\) とし、\(3\) 以上の奇数であるものを降順に並べたものを \(S_{odd}\) とします。また、\(1\) の数を \(K\) とします。
\(A_{0}\) の値で場合分けして答えを求めます。
\(0\leq A_{0}\leq \dfrac{\sum S_{even}}{2}\) であるとき
\(S_{even}\) の部分列 \(T\) であって、\(A_{0} = \dfrac{\sum T}{2}\) であるものが存在するならば、\((C[2]_{A_{0}}, C[1]_{A_{0}}, Y_{A_{0}}) = (A_{0}, 0, 0)\) となります。
これは \(T\) に含まれるサイズの連結成分のサイクルについて、\((0, 2, 0, 2, \dots)\) と交互に並べることで達成できます。
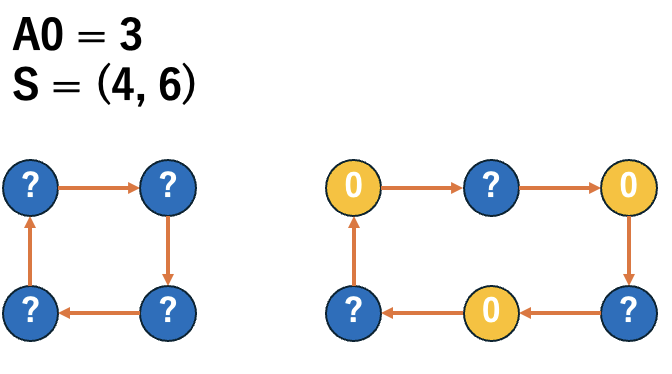
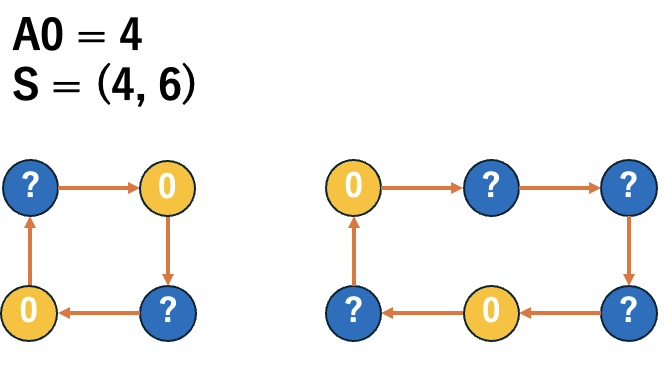
逆に上記のような \(T\) が存在しないならば、\((C[2]_{A_{0}}, C[1]_{A_{0}}, Y_{A_{0}}) = (A_{0} - 1, 2, 0)\) となります。
これは偶数サイクルに \((0, 2,\dots, 0, 2)\) を順番に入れて、\(0\) が足りなくなったら、\((0, 2, 0, 2, 2, 2, 2, \dots)\) のようにすればいいです。
\(\dfrac{\sum S_{even}}{2} < A_{0}\leq \dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} - |S_{odd}|}{2}\) であるとき
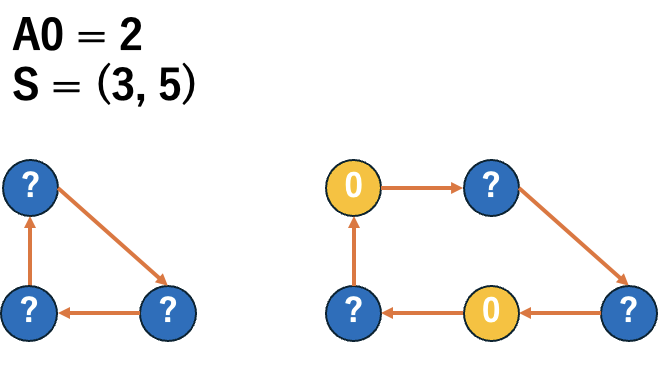
\(A_{0} - \dfrac{\sum S_{even}}{2}\leq\dfrac{\sum_{i = 1}^{k} S_{odd}[i] - k}{2}\) を満たす最小の \(k\) を用いて、\((C[2]_{A_{0}}, C[1]_{A_{0}}, Y_{A_{0}}) = (A_{0} - k, 2k, 0)\) となります。
これは偶数サイクルに \((0, 2, \dots , 0, 2)\) と埋めた後、奇数サイクルに \((0, 2, 0, \dots, 0, 2, 0)\) のように大きい順に埋めていけばいいです。
\(\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} - |S_{odd}|}{2}<A_{0}\leq \dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2}\) であるとき
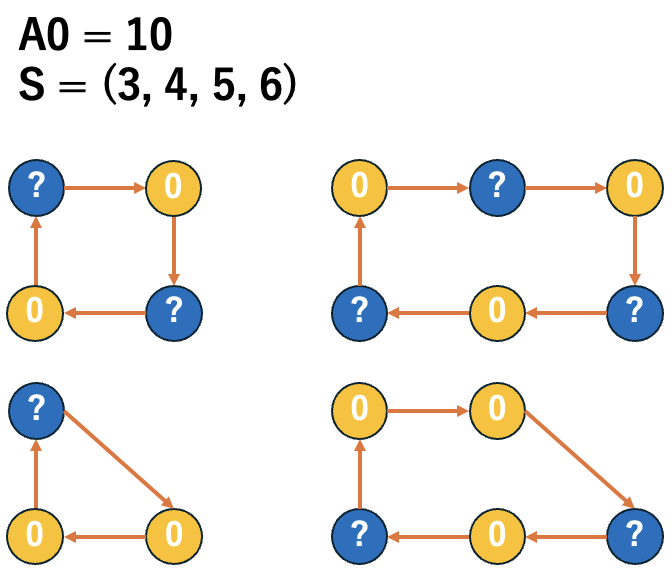
\(r = A_{0} - \dfrac{\sum S_{even}}{2} - \dfrac{\sum S_{odd} - |S_{odd}|}{2}\) として、\((C[2]_{A_{0}}, C[1]_{A_{0}}, Y_{A_{0}}) = (A_{0} - |S_{odd}|, 2(|S_{odd}| - r), r)\) となります。
これは例えば \(S_{i} = 5\) のとき、 \((2, 0, 2, 0, 2)\) と埋めていたものを \((0, 2, 0, 2, 0)\) と変更することを \(S_{odd}\) の各要素に対して行えばいいです。
\(\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2}<A_{0}\leq \dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2} + K\) であるとき
\((C[2]_{A_{0}}, C[1]_{A_{0}}, Y_{A_{0}}) = (\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} - |S_{odd}|}{2}, 0, A_{0} - \dfrac{\sum S_{even}}{2} - \dfrac{\sum S_{odd} - |S_{odd}|}{2})\) となります。
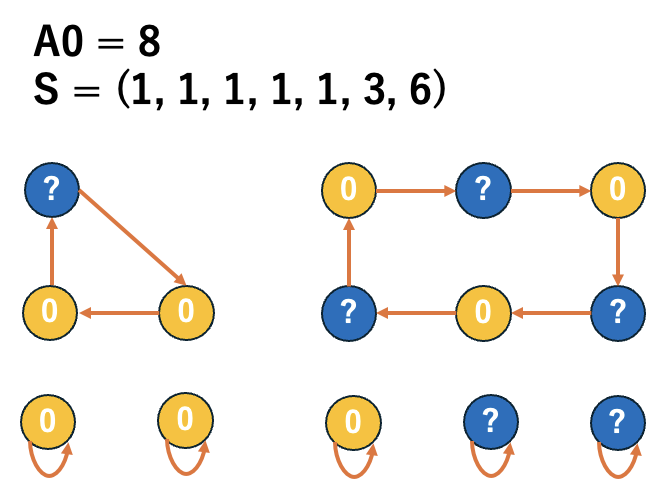
\(\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2} + K<A_{0}\leq N\) であるとき
\((C[2]_{A_{0}}, C[1]_{A_{0}}, Y_{A_{0}}) = (N - A_{0}, 0, 2A_{0} - N)\) となります。
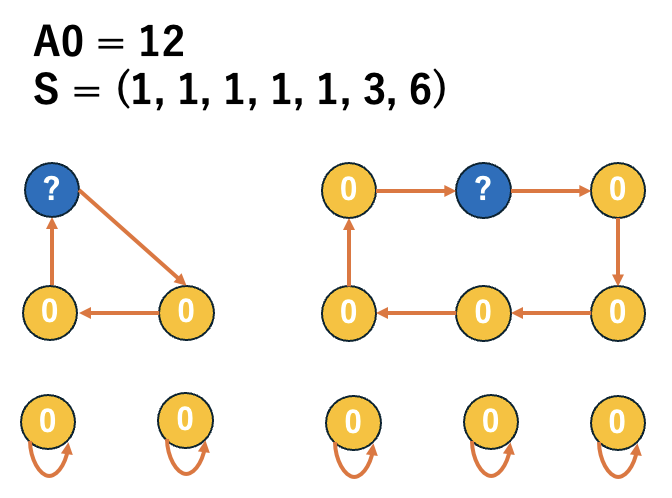
以上が \(0\) 以上 \(N\) 以下の \(A_{0}\) 全てに対する \((C[2]_{A_{0}}, C[1]_{A_{0}}, Y_{A_{0}})\) のひとつです。\(0\leq A_{0}\leq \dfrac{\sum S_{even}}{2}\) であるときの答えを求める部分以外は \(N\) に対して線形時間で求めることができます。\(0\leq A_{0}\leq \dfrac{\sum S_{even}}{2}\) であるときの答えを求める部分は、\(S_{even}\) に含まれる種類数が \(O(\sqrt{N})\) であることを用いて、時間計算量 \(O(N\sqrt{N})\) で求められます。(bitset を用いてさらに高速化することも可能です)
実装例
posted:
last update: