 /
/ 
実行時間制限: 3 sec / メモリ制限: 1024 MiB
配点 : 800 点
問題文
2 次元平面上に 1,2, \dots, N の番号がついた N 個の点があります。 点 i の座標は (i,Y_i) です。 なお、この問題では Y=(Y_1,Y_2,\dots ,Y_N) は (1,2, \dots ,N) の順列であることが保証されます。
\lbrace \texttt{点} 1,\texttt{点} 2,\dots ,\texttt{点} N \rbrace の要素数 2 以上の部分集合 S 全てに対するバウンディングボックスの面積の総和を 998244353 で割った余りを求めて下さい。
S に対するバウンディングボックスとは、 S に含まれる全ての点を内部または周上に含んでかつ x 軸に平行な辺を持つような長方形のうち、面積が最小であるものを指します。
制約
- 2 \le N \le 2 \times 10^5
- Y は (1,2, \dots ,N) の順列
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Y_1 Y_2 \ldots Y_N
出力
バウンディングボックスの面積の総和を 998244353 で割った余りを出力せよ。
入力例 1
4 2 3 1 4
出力例 1
50
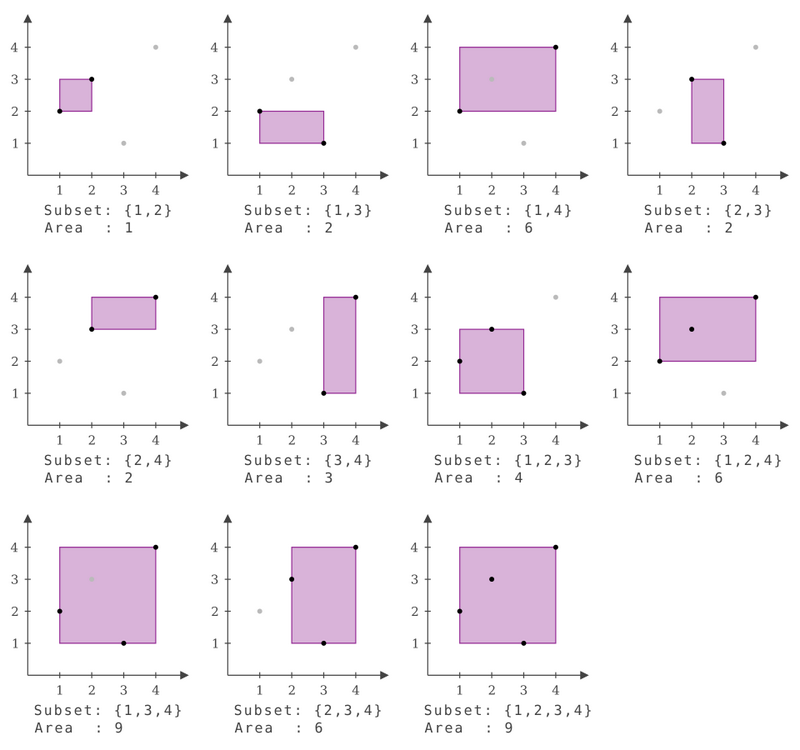
各部分集合とバウンディングボックスの面積は下図の通りです。面積の総和である 50 を出力します。
入力例 2
26 6 14 8 19 13 25 26 22 7 3 16 15 11 24 1 12 20 23 5 17 9 2 21 10 4 18
出力例 2
575187918
Score : 800 points
Problem Statement
There are N points numbered 1,2, \dots, N on the 2-dimensional plane. The coordinates of point i are (i,Y_i). In this problem, it is guaranteed that Y=(Y_1,Y_2,\dots ,Y_N) is a permutation of (1,2, \dots ,N).
Find the sum of the areas of bounding boxes for all subsets S of \lbrace \texttt{point}\,1,\texttt{point}\,2,\dots ,\texttt{point}\,N \rbrace with at least 2 elements, modulo 998244353.
The bounding box for S refers to the minimum area rectangle with sides parallel to the x-axis that contains all points in S inside or on the boundary.
Constraints
- 2 \le N \le 2 \times 10^5
- Y is a permutation of (1,2, \dots ,N).
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Y_1 Y_2 \ldots Y_N
Output
Output the sum, modulo 998244353, of the areas of bounding boxes.
Sample Input 1
4 2 3 1 4
Sample Output 1
50
Each subset and the area of its bounding box are shown in the figure below. Output the sum of areas, which is 50.

Sample Input 2
26 6 14 8 19 13 25 26 22 7 3 16 15 11 24 1 12 20 23 5 17 9 2 21 10 4 18
Sample Output 2
575187918