解法

Div.1,Div.2,Div.3 をそれぞれ \(x,y,z\) セット組めるような \((x,y,z)\) の組について \(3\) 次元空間の格子点 \((x,y,z)\) を考え、その集合を \(S\) とします。

結論から言うと、\(S\) はある整数 \(R_x,R_y,R_z,R_{xy},R_{xz},R_{yz},R_{xyz}\) について、以下の不等式を全て満たす全ての格子点 \((x,y,z)\) からなる集合です。（連続緩和問題が凸多面体のミンコフスキー和であることを考えると自然な発想と言えるでしょう。）

• \(0 \le x \le R_x\)
• \(0 \le y \le R_y\)
• \(0 \le z \le R_z\)
• \(x+y \le R_{xy}\)
• \(x+z \le R_{xz}\)
• \(y+z \le R_{yz}\)
• \(x+y+z \le R_{xyz}\)

つまり、\(R_x \dots R_{xyz}\) を管理しておくことで、開催出来る C3C の回数を \(min(R_x,R_y,R_z,\lfloor \frac{R_{xy}}{2} \rfloor,\lfloor \frac{R_{xz}}{2} \rfloor,\lfloor \frac{R_{yz}}{2} \rfloor,\lfloor \frac{R_{xyz}}{3} \rfloor)\) と求めることが出来ます。

writer を追加するとき、\(R_x \dots R_{xyz}\) をそれぞれ独立に更新すればよいです。更新式の例は以下の通りです。

• \(R_x = R_x+min(A_i,B_i,C_i)\)
• \(R_{xy} = R_{xy}+min(A_i+D_i,B_i,C_i)\)
• \(R_{xz} = R_{xz}+min(min(A_i,B_i)+min(D_i,E_i),C_i)\)
• \(R_{xyz} = R_{xyz}+min(A_i+D_i,B_i+E_i,B_i+D_i,C_i)\)

計算量は \(O(N)\) です。（コード）

証明

上記の解法で求めた値が上界であることは明らかなので、下界であることを示します。

\(S\) に \((x,y,z)\) が含まれる時、\((x-1,y,z), (x,y-1,z), (x,y,z-1)\) も（座標が負にならないならば）\(S\) に含まれます。

極大な点集合、つまり \((x+1,y,z), (x,y+1,z), (x,y,z+1)\) がいずれも \(S\) に含まれないような \(S\) の点全てからなる集合 \(T\) について考えます。

\(T\) のうち \(y\) が最大の点 \(P=(x_P,y_P,z_P)\) は一意に定まります。なぜなら、Div.2 を最大限に組んだとき、各 writer の問題案は Hard,Medium,Easy のいずれかが \(0\) 個になるため Div.1 または Div.3 のいずれかしか組むことが出来ず、\(x,z\) の最大値が独立に一意に定まるためです。

\(P\) から \(y\) を \(1\) ずつ減らして行くと、はじめは \(x,z\) 両方を \(1\) ずつ増やすことが出来（回数の上限を \(C_{xz}\) とします）、どこかの時点から \(x,z\) のうち片方しか \(1\) 増やすことが出来なくなります。\(x,z\) を \(1\) 増やすことが出来る回数にはそれぞれ上限（\(C_x,C_z\) とします）があり、その合計にも上限（\(C_{sum}\) とします）があります。\(C_{xz},C_x,C_z,C_{sum}\) はそれぞれこのコードのように貪欲に求めることが出来ます。

下図は \(S,T,P,C_{xz},C_x,C_z,C_{sum}\) の例を図示したものです。

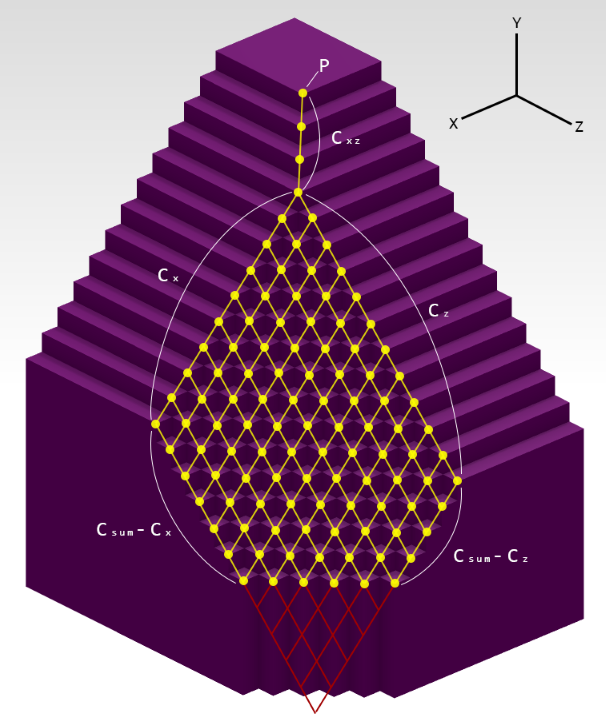
このような \(T\) を持つ \(S\) は上記の解法のような \(R_x,R_y,R_z,R_{xy},R_{xz},R_{yz},R_{xyz}\) で表せるような点集合となります。\(S\) の点が全て実現可能であることは構成的に示されており、下界であることが示されました。