操作によって得られる行列を 良い行列 と呼ぶことにします．まずは良い行列の個数の求め方を考えます．

次の手順で良い行列を生成します．

• \(0\) 以上 \(W\) 以下の整数からなる長さ \(H\) の数列 \(R\)，および \(0\) 以上 \(H\) 以下の整数からなる長さ \(W\) の数列 \(C\) を用意する．\(1\leq i\leq H,1\leq j\leq W\) に対し，\(j\leq R_i\) または \(i\leq C_j\) ならば \(A_{i,j}=1\) ，そうでないなら \(A_{i,j}=0\) とする．

ある良い行列 \(A\) を生成するような \(R,C\) は一般に複数ありますが，その中で \(C\) が辞書順最大のもの，さらにその中で \(R\) が辞書順最大のものと限定したものを考えます．この関係が成り立っている \(R,C\) を すばらしい関係 と呼びます．すばらしい関係である \(R,C\) と良い行列 \(A\) は一対一対応します．すばらしい関係である \(R,C\) とそれから生成される \(A\) について，以下が分かります．

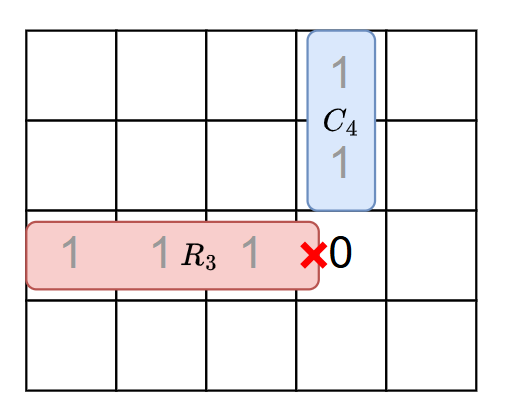
• \(C_j\neq H\) のとき，\(A_{C_j+1,j}=0\) である．よって \(R_{C_{j}+1}\lt j\) である．
  
  • 下図の例では，\(C_4=2\) であることより \(A_{4,3}=0,R_3\lt 4\) が成り立つ．

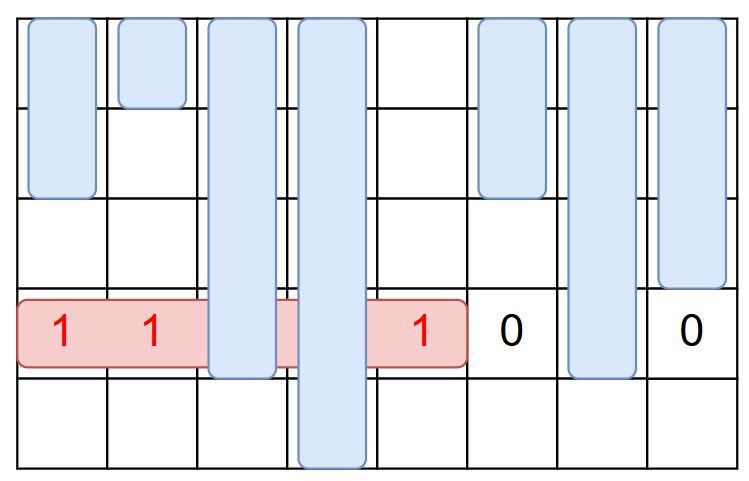
• \(C_j\lt i\) であるような \(j\) を順に \(j_1,j_2,\ldots\) とする．このとき，\(A_{i,j_1},A_{i,j_2},\ldots\) は単調減少である．
  • 下図の例では，\(C_j\lt 4\) となる \(j\) は \(j=1,2,5,6,8\) であり，\(A_{4,1}\geq A_{4,2}\geq A_{4,5}\geq A_{4,6}\geq A_{4,8}\) である．

これらを踏まえると， \(C\) が決まっているとき，その \(C\) とすばらしい関係になるような \(R\) の個数を求めることができます．すばらしい関係になる \(R\) について，各 \(R_i\) の値は独立に決めることができます：

• \(C_j=i-1\) が成り立つような最小の \(j\) を \(L\) とする（存在しなければ \(L=W+1\)）．\(1\leq j\lt L\) のうち \(A_j\lt i\) を満たす個数を \(d_i\) としたとき，\(R_i\) の決め方は \(d_i+1\) 通り存在する

各 \(C\) に対するすばらしい関係であるような \(R\) の個数の求め方をもとに，すべての \(C\) に対するすばらしい関係であるような \(R\) の個数の総和を求めることにします．これは，\(C_j\lt i\) となる \(j\) の個数に着目して分類すると良いです．

行 \(i\) から \(i+1\) に移る際，\(C_j=i\) となる \(j\) が存在したとします．そのような列が，\(C_j\lt i\) であるような列たちとどのような相対関係にあるのかが重要です．より具体的には，\(C_j=i\) となる列たちが \(C_j\lt i\) となる列たちのどこに挿入されるかによって，\(1\) を置くことができる場所の個数が変わります．

• 下図は，挿入する位置によって \(1\) を置くことができる場所の数（\(=d_i\)）が変化することを示しています．

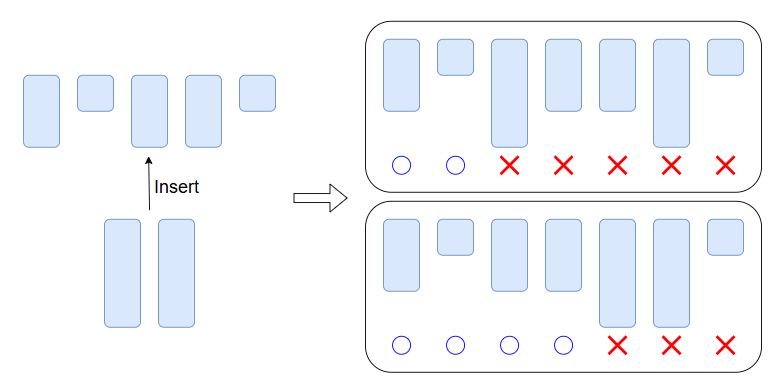
一番左に挿入される列の場所に応じて，

• \(1\) をどこまで右に伸長できるか
• 残りの挿入する列をどこに挿入するか

をそれぞれ自由に決めることができます．

これを dp で計算します．\(\mathrm{dp}[i][k]\) を次の組の決める方法の総数とします．

• \(C\) のうち \(i\) 未満であるようなもののみを取り出した部分列 \(C'\)（長さ \(k\)）
• \(i\) 行目までの各行で，左からいくつ \(1\) を伸ばすか
  • これは，\(i'=1,2,\ldots,i\) に対して，\(C'_j=i'-1\) が成り立つような最小の \(j\) を \(L'\) （存在しなければ \(L'=k+1\)），\(1\leq j\lt L'\) のうち \(A_j\lt i'\) を満たす個数を \(d'_{i'}\) としたとき， \(\prod_{i'=1}^i (d'_{i'}+1)\) 通り存在する

\(C_j\lt i\) を満たす \(j\) の個数が \(k_1\)，\(C_j\lt i+1\) を満たす \(j\) の個数が \(k_2\ (k_1\lt k_2)\) だったとき，\(k_2\) 箇所の中でどこを挿入する一番左にするかを決める（場所を \(l\) とする）と

• 左から \(1\) をどれだけ伸ばせるか（\(l\) 通り）
• 挿入する残りの \(k_2-k_1-1\) 個を \(l\) より右の \(k_2-l\) 個の中のどこにするか（\(\binom{k_2-l}{k_2-k_1-1}\) 通り）

の自由度があります．よって，\(\displaystyle \mathrm{dp}[i+1][k_2]\leftarrow \mathrm{dp}[i][k_1]\times \sum_{l=1}^{k_2} l\times \binom{k_2-l}{k_2-k_1-1}=\mathrm{dp}[i][k_1]\times \binom{k_2+1}{k_1}\) という遷移をたどります．（この遷移式は \(k_1=k_2\) のときも同じになります．）（二項係数の式変形をせずに前計算 \(O(W^3)\) かけて遷移行列を求めても構いません．）

よって，\(O(HW^2)\) で \(\mathrm{dp}[H][\ast]\) を求めることができます．\(C_j=H\) を満たす \(j\) が存在したとき，その列たちを \(C_j\lt H\) となる列たちのどこに挿入するかを決められることを踏まえると，最終的にすばらしい関係が成り立つ \(R,C\) の組（すなわち良い行列 \(A\)）の個数は \(\displaystyle \sum_{j=0}^W \mathrm{dp}[H][j]\times \binom{W}{j}\) です．

これと全く同じ考え方で良い行列全てに対する \(\sum A_{i,j}\) の総和も求めることができます．

\(H<W\) の場合は \(H,W\) を入れ替えても良いため，計算量 \(O(HW\min(H,W))\) でこの問題を解くことができます（畳み込みで \(O(HW\log \min(H,W))\) に落とすことも可能です）．

mod = 998244353
fac = [1] * 1000
for i in range(1, 1000):
    fac[i] = fac[i - 1] * i % mod
finv = [pow(fac[i], mod - 2, mod) for i in range(1000)]


def binom(n, k):
    if n < 0 or k < 0 or k > n:
        return 0
    return fac[n] * finv[k] % mod * finv[n - k] % mod


H, W = map(int, input().split())
if H < W:
    H, W = W, H

dp = [[0] * (W + 1) for i in range(H + 1)]
cnt = [[0] * (W + 1) for i in range(H + 1)]
dp[0][0] = 1
for i in range(H):
    for j in range(W + 1):
        for k in range(j, W + 1):
            dp[i + 1][k] = (dp[i + 1][k] + dp[i][j] * binom(k + 1, j)) % mod
            cnt[i + 1][k] = (cnt[i + 1][k] + cnt[i][j] * binom(k + 1, j) + dp[i][j] * binom(k + 1, j - 1)) % mod
        cnt[i + 1][j] = (cnt[i + 1][j] + dp[i + 1][j] * (W - j)) % mod
print(sum(cnt[H][i] * binom(W, i) % mod for i in range(W + 1)) % mod)

---

（作問裏話）

この問題は，私と sotanishy 君を含む数人で埼玉県の秩父を訪れた際に，sotanishy 君が秩父駅から見える石灰岩の山肌を見て「長方形のグリッドを削る問題が作れないかなあ」と発言したことをきっかけに作られました．問題名はこのエピソードに由来しています．