 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 800 点
問題文
正整数 N, H, W が与えられます.ただし,H, W \leq 3N-1 が成り立ちます.
H\times W のマス目に N\times N の正方形のタイルを 4 個置く方法であって,以下の条件をすべて満たすものの個数を 998244353 で割った余りを求めてください.
- 各タイルは,マス目の ちょうど N^2 個のマスを完全に覆う.
- ひとつのマスが複数のタイルによって覆われてはならない.
ただし,タイル同士は区別しません.
T 個のテストケースが与えられるので,それぞれについて解いてください.
制約
- 1\leq T\leq 2\times 10^5
- 1\leq N,H,W\leq 10^9
- H,W\leq 3N - 1
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられます.
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられます.
N H W
出力
T 行出力してください.i 行目には i 番目のテストケースについて,条件を満たすようにタイルを置く方法の個数を 998244353 で割った余りを出力してください.
入力例 1
4 2 4 5 2 5 5 1000 1000 1000 1000 2222 2025
出力例 1
9 79 0 262210557
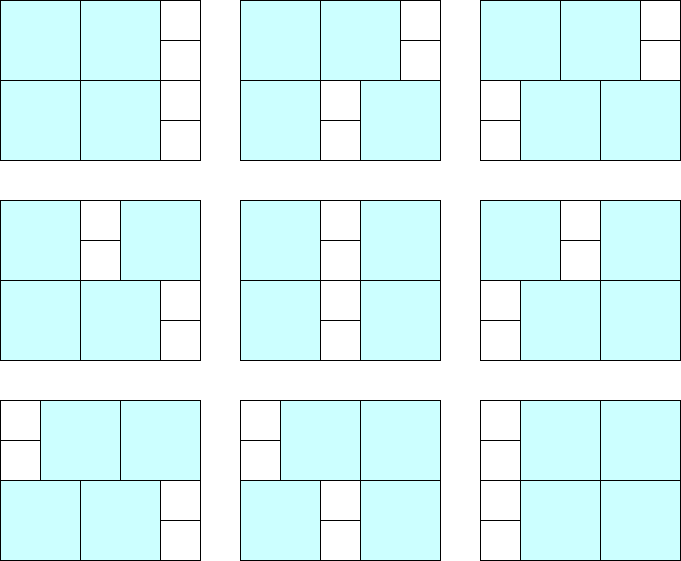
1 つめのテストケースについて,次の図で示す 9 通りの方法があります.
Score : 800 points
Problem Statement
You are given positive integers N, H, and W, with H,W \le 3N-1.
Find the number, modulo 998244353, of ways to place four N\times N square tiles on an H\times W grid that satisfy all of the following conditions.
- Each tile exactly covers N^2 cells of the grid.
- No cell is covered by more than one tile.
Here, the tiles are indistinguishable.
There are T test cases; solve each one.
Constraints
- 1\le T\le 2\times 10^5
- 1\le N,H,W\le 10^9
- H,W\le 3N-1
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
N H W
Output
Print T lines. The i-th line should contain the number, modulo 998244353, of valid ways to place the tiles for the i-th test case.
Sample Input 1
4 2 4 5 2 5 5 1000 1000 1000 1000 2222 2025
Sample Output 1
9 79 0 262210557
For the first test case, there are 9 ways as illustrated in the following figure:
