 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 700 点
問題文
N\times N 行列 A = (A_{i,j}) (1\leq i,j\leq N) が与えられます.A の成分は 0 または 1 です.
頂点に 1 から N までの番号が付けられた N 頂点の木 G であって,次の条件を満たすものの個数を 998244353 で割った余りを求めてください.
- A_{i,j}=1 であることと,以下の 2 条件のうち少なくともひとつが成り立つことは同値である:
- 頂点 1 を根としたとき頂点 j は頂点 i の祖先である.つまり頂点 j は,頂点 1, i を結ぶ G 上のパス上にある.
- 頂点 1 を根としたとき頂点 i は頂点 j の祖先である.つまり頂点 i は,頂点 1, j を結ぶ G 上のパス上にある.
ただし,パスの端点もパス上にあると見なします.G は木であるとき,2 頂点を結ぶ G 上のパスは一意に存在することにも注意してください.
T 個のテストケースが与えられるので,それぞれについて解いてください.
制約
- 1\leq T\leq 10^5
- 2\leq N\leq 400
- A_{i,j}\in \lbrace 0,1\rbrace (1\leq i,j\leq N)
- A_{i,i}=1 (1\leq i\leq N)
- A_{i,j}=A_{j,i} (1\leq i,j\leq N)
- すべてのテストケースにわたる N^2 の総和は 400^2 以下.
入力
入力は以下の形式で標準入力から与えられます.
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられます.
N
A_{1,1} \cdots A_{1,N}
\vdots
A_{N,1} \cdots A_{N,N}
出力
T 行出力してください.i 行目には i 番目のテストケースについて,条件を満たす N 頂点の木 G の個数を 998244353 で割った余りを出力してください.
入力例 1
5 3 1 1 1 1 1 0 1 0 1 3 1 1 1 1 1 1 1 1 1 3 1 0 0 0 1 0 0 0 1 3 1 0 1 0 1 1 1 1 1 7 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 1 1
出力例 1
1 2 0 0 8
1 番目のテストケースでは次の 1 つの G が条件を満たします.
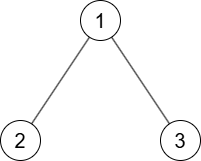
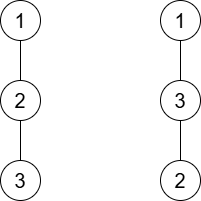
2 番目のテストケースでは次の 2 つの G が条件を満たします.
Score : 700 points
Problem Statement
You are given an N\times N matrix A = (A_{i,j}) (1\le i,j\le N) whose entries are 0 or 1.
Find, modulo 998244353, the number of trees G on N vertices numbered 1 to N that satisfy the following condition.
- A_{i,j}=1 if and only if at least one of the following holds:
- When G is rooted at vertex 1, Vertex j is an ancestor of vertex i. That is, vertex j lies on the unique path in G between vertices 1 and i.
- When G is rooted at vertex 1, Vertex i is an ancestor of vertex j. That is, vertex i lies on the unique path in G between vertices 1 and j.
Here, the endpoints of a path are considered to be on that path. Note that G being a tree guarantees uniqueness of the path between any two vertices.
There are T test cases; solve each one.
Constraints
- 1\leq T\leq 10^5
- 2\leq N\leq 400
- A_{i,j}\in \lbrace 0,1\rbrace (1\leq i,j\leq N)
- A_{i,i}=1 (1\leq i\leq N)
- A_{i,j}=A_{j,i} (1\leq i,j\leq N)
- The sum of N^2 over all test cases is at most 400^2.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
N
A_{1,1} \cdots A_{1,N}
\vdots
A_{N,1} \cdots A_{N,N}
Output
Print T lines. The i-th line should contain the number, modulo 998244353, of trees G satisfying the conditions for the i-th test case.
Sample Input 1
5 3 1 1 1 1 1 0 1 0 1 3 1 1 1 1 1 1 1 1 1 3 1 0 0 0 1 0 0 0 1 3 1 0 1 0 1 1 1 1 1 7 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 1 1
Sample Output 1
1 2 0 0 8
In the first test case, the following one tree G satisfies the condition:

In the second test case, the following two trees G satisfy the condition:
