 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 400 点
問題文
H\times W のマス目があります.上から h 行目,左から w 列目のマスを (h,w) で表します.さらに,D, R, ? からなる長さ H+W-2 の文字列 S=S_1\cdots S_{H+W-2} が与えられます.
はじめ,すべてのマスは白色で塗られています.あなたは次の 3 つの手順からなる操作を何度でも行うことができます:
- 以下の条件をすべて満たす長さ H+W-2 の文字列 X=X_1\cdots X_{H+W-2} をひとつ選ぶ.
- X は H-1 個の
Dおよび W-1 個のRからなる. - 1\leq i\leq H+W-2 に対して,S_i が
Dならば X_i もDである. - 1\leq i\leq H+W-2 に対して,S_i が
Rならば X_i もRである.
- X は H-1 個の
- マス (1,1) に立つ.さらに i=1,2,\ldots の順に,文字 X_i の表す方向に 1 マス移動する.つまり,X_i が
Dならば下方向,X_i がRならば右方向に 1 マス移動する.なお,X が手順 1 の条件を満たすとき,移動先のマスは必ずマス目内に存在することが証明できる. - 手順 2 においてあなたが通ったすべてのマス(最初・最後のマスも含む)について,そのマスが白色で塗られているならば,黒色で塗る.
最終的に黒色で塗ることができるマスの個数としてありうる最大値を求めてください.
T 個のテストケースが与えられるので,それぞれについて解いてください.
制約
- 1\leq T\leq 2\times 10^5
- 2\leq H, W\leq 2\times 10^5
- T,H,W は整数.
- S は
D,R,?からなる長さ H+W-2 の文字列. - S に含まれる
Dの個数は H-1 以下. - S に含まれる
Rの個数は W-1 以下. - すべてのテストケースにわたる H+W の総和は 4\times 10^5 以下.
入力
入力は以下の形式で標準入力から与えられます.
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられます.
H W S
出力
T 行出力してください.i 行目には i 番目のテストケースについて,最終的に黒色で塗ることができるマスの個数としてありうる最大値を出力してください.
入力例 1
4 4 5 D?DRR?R 4 5 DDRRDRR 4 5 ??????? 2 2 DR
出力例 1
12 8 20 3
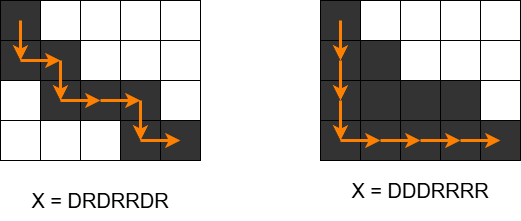
1 つめのテストケースについて,1 回目に X として DRDRRDR を選び,2 回目に X として DDDRRRR を選ぶことで,12 個のマスを黒く塗ることができます.
Score : 400 points
Problem Statement
There is an H\times W grid of cells. Let (h,w) denote the cell at the h-th row from the top and the w-th column from the left. Furthermore, you are given a string S = S_1\cdots S_{H+W-2} of length H+W-2 consisting of D, R, and ?.
Initially, all cells are painted white. You may perform the following operation, which consists of three steps, any number of times:
- Choose a string X = X_1\cdots X_{H+W-2} of length H+W-2 satisfying all of the following.
- X consists of exactly H-1
Ds and W-1Rs. - For each 1 \le i \le H+W-2, if S_i is
Dthen X_i must also beD. - For each 1 \le i \le H+W-2, if S_i is
Rthen X_i must also beR.
- X consists of exactly H-1
- Stand on cell (1,1). Then for i=1,2,\ldots in order, move one cell in the direction indicated by X_i: if X_i is
D, move down one cell; if X_i isR, move right one cell. It can be shown that if X satisfies the conditions in step 1, the destination cell always exists within the grid. - For every cell you visited in step 2 (including the starting and ending cells), if the cell is currently white, paint it black.
Find the maximum possible number of cells that can be painted black in total.
There are T test cases; solve each one.
Constraints
- 1\le T\le 2\times 10^5
- 2\le H,W\le 2\times 10^5
- T,H,W are integers.
- S is a string of length H+W-2 consisting of
D,R, and?. - The number of
Ds in S is at most H-1. - The number of
Rs in S is at most W-1. - The sum of H+W over all test cases is at most 4\times 10^5.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
H W S
Output
Print T lines. The i-th line should contain the maximum number of cells that can be painted black for the i-th test case.
Sample Input 1
4 4 5 D?DRR?R 4 5 DDRRDRR 4 5 ??????? 2 2 DR
Sample Output 1
12 8 20 3
For the first test case, by choosing X as DRDRRDR in the first operation and DDDRRRR in the second operation, you can paint 12 cells black.
