ヒント集 → https://atcoder.jp/contests/arc197/editorial/12811

[1] 祖先・子孫関係で定まるグラフの観察

本解説では，入力で与えられる行列をグラフと解釈して解説します．つまり，\(i\neq j\) に対して \(A_{i,j}=1\) のときに \(i\) と \(j\) を結んでできるグラフです．

根付き木 \(G\) に対して，本問のように \(G\) の祖先・子孫の関係により定まるグラフ（ただしループは除外）を \(f(G)\) と書くことにします．

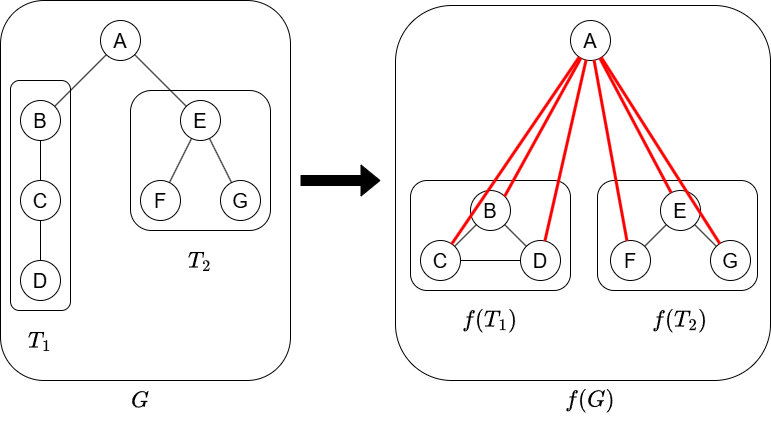
根付き木 \(G\) がを根 \(r\) に部分木 \(T_1, \ldots, T_k\) をつけたものだとすると，\(f(G)\) は次のようにして得られます．

• \(f(T_1), \ldots, f(T_k)\) を求める．その後，\(r\) とすべての頂点を結ぶ．

[2] 数え上げ

\(f(G)\) だけが与えられたとき，\(G\) を復元するにはどうすればよいでしょうか？これは，上で述べた \(f\) の計算方法を逆順に辿ればよいです．つまり，

• すべての頂点と隣接する頂点を根として選ぶ．
• その頂点を除き連結成分に分解する．各連結成分ごとに根付き木 \(T_k\) を復元し，根につなげる．

とすればよいです．

この際，「すべての頂点と隣接する頂点」の選び方に任意性があります（選び方が存在しない場合答は \(0\) です）．そのような頂点が複数あるときには，どの頂点を選んだ場合も，その後の計算には影響しないので，候補の個数を答にかけて，あとは特定の候補を選んだ場合について再帰的な計算を行えばよいです．

あるいはそれをまとめて行って，候補の個数の階乗を答にかけたあと候補をすべて除くという実装をすることもできます．

本問では最初にそのような頂点を選ぶ場合のみ，頂点 \(1\) を選ぶ必要があることにも注意してください．

以上のことを実装すれば，\(O(N^3)\) などの計算量で答を求めることができます．

• 解答例：https://atcoder.jp/contests/arc197/submissions/65381404