Overall Editorial by maspy

ヒント集

A - Union of Grid Paths

Hint 1

マス $(x,y)$ を黒く塗ることができるのは，$(1,1)$ から $(x,y)$ までの部分，$(x,y)$ から $(H,W)$ までの部分がそれぞれ移動できる場合です．

Hint 2

$k$ を固定して，$x+y=k$ を満たす $(x,y)$ の個数を計算する方法を考えましょう．

Hint 1

最適解に仮定できる性質を探します．そのために，部分列に対する操作（要素の追加削除や交換）であってスコアを減らさないものを探しましょう．

Hint 2

平均値以下の要素で選ばれていないものがあるならば，これを追加する操作はスコアを減らしません．したがって，平均値以下の要素はすべて選ばれている場合だけを考えればよいです．

Hint 3

平均値以上の要素についてはどうでしょうか？選ばれているものと選ばれていないものを交換することを考えてみましょう．

Hint 1

問題文に「$S$ はこの時点で $B_i$ 個以上の要素を含むことが証明できる」と書かれていますが，まずはこの証明を考えてみましょう．

Hint 2

答はあまり大きくなく，例えば $3\times 10^6$ 以下であることが証明できます．この範囲の数に対して削除および $k$ 番目の取得ができるデータ構造を用意します．

Hint 3

同じ数の倍数を何度も調べたり,　同じ数を何度もデータ構造から削除してしまうと計算量がオーダーレベルで悪くなる可能性があるので注意してください．

Hint 1

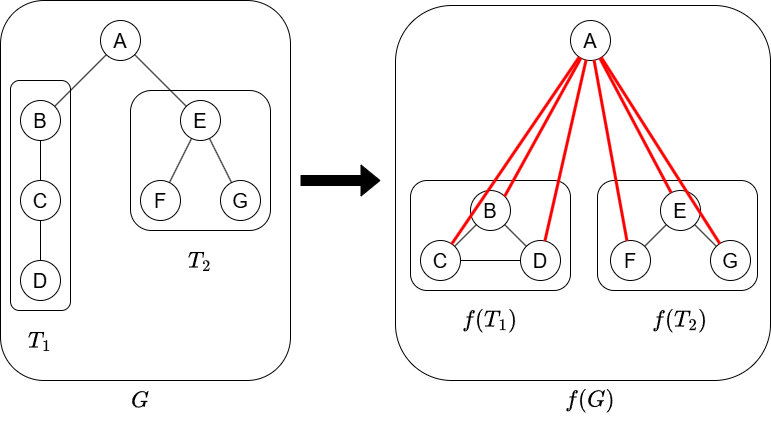
入力で与えられるものは行列というよりも，グラフと思った方が分かりやすいと思います．まずは根付き木に対するグラフがどのようなものかを考えましょう．

Hint 2

Hint 3

入力のグラフから根付き木を復元するには，「全頂点と隣接する頂点を選び根とする」「根を削除し連結成分分解する」を繰り返せばよいです．

Hint 1

左上・右上・左下・右下にひとつずつタイルを置くという位置関係になります．

Hint 2

まずは隣同士のタイルが重ならないような置き方を数えましょう．そこから余分に数えているものを引きます．

Hint 3

隣同士のタイルが重ならない場合，「左上と右下」「右上と左下」どちらもが重なることはありません．よってどちらかが重なってしまう場合を数えればよいです．条件を整理すると，行・列それぞれ独立に計算できることが分かります．

posted:
last update: