Step 1

Solving the general case directly is difficult, so let’s first consider solving Sample Input 1 manually.

5
RBRBB
RBRRR
RRRBR
RBBRB
BBRBR

The original problem requires considering the following two conditions simultaneously, which is quite complex and difficult even for a grid of about \(5 \times 5\) size as in Sample Input 1.

• Condition 1: You can move from the top-left to the bottom-right only passing through cells that are red or purple.
• Condition 2: You can move from the top-right to the bottom-left only passing through cells that are blue or purple.

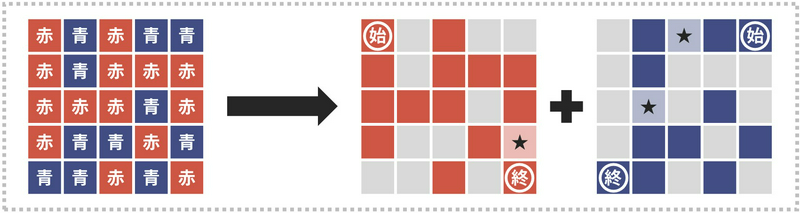
Therefore, let’s consider dividing the grid into two as shown in the figure below. The red cells correspond to the state where only the left side is painted, and the blue cells correspond to the state where only the right side is painted. Although not shown in the figure, the purple cells correspond to the state where both sides are painted.

[The kanji below mean the following. 赤: red, 青: blue, 始: start, 終: end]

Then, the operation of changing a cell from red or blue to purple can be rephrased as the operation of painting one cell in one of the two divided grids. The specific correspondence is as follows.

• Blue → Purple: Paint an unpainted cell in the left grid.
• Red → Purple: Paint an unpainted cell in the right grid.

Also, Conditions 1 and 2 can be rephrased as follows:

• Condition 1: You can move from the top-left to the bottom-right only passing through painted cells in the left grid.
• Condition 2: You can move from the top-right to the bottom-left only passing through painted cells in the right grid.

In other words, the “Blue → Purple operation” only affects Condition 1, and the “Red → Purple operation” only affects Condition 2.

Therefore, to satisfy Condition 1, one “Blue → Purple operation” is necessary (see the star in the middle figure), and to satisfy Condition 2, two “Red → Purple operations” are necessary (see the stars in the right figure), so we can see that the answer is \(1+2=3\). By considering the two operations separately and independently, we were able to solve it easily by hand.

---

Step 2

So far, we have explained how to solve Sample Input 1, but how can we solve the general case?

First, similar to Sample Input 1, by dividing the grid into two, we can consider red and blue independently, so if we can solve the problem for red, we can simply add the results to solve this problem. In other words, given a grid painted with red or white, how many cells need to be repainted red to enable movement from the top-left to the bottom-right?

An important property here is that the minimum number of cells that need to be repainted red is the same as the minimum number of white cells that need to be passed to move from the top-left to the bottom-right. For example, consider the case shown in the figure below. Indeed, they are both “one”.

• By repainting a minimum of one cell red, you can move from the top-left to the bottom-right.
• To move from the top-left to the bottom-right, you need to pass through a minimum of one white cell.

Proof that they are the same

• Let \(a\) be the minimum number of cells that need to be repainted red to enable movement from the top-left to the bottom-right.
• Let \(b\) be the minimum number of white cells that need to be passed to move from the top-left to the bottom-right.
• The following can prove \(b \geq a\).
  • Consider a path that passes through \(b\) white cells.
  • If all white cells on this path are repainted red, it becomes possible to move from the top-left to the bottom-right.
  • This means that it becomes possible to move from the top-left to the bottom-right with \(b\) repaintings.
  • Therefore, \(b \geq a\).
• The following can prove \(b \leq a\).
  • Consider a method that allows movement from the top-left to the bottom-right with \(a\) repaintings.
  • Let the path after repainting be \(S\).
  • At this time, the path \(S\) contains at most \(a\) cells that were originally white.
  • This means that it is possible to move from the top-left to the bottom-right without passing through more than \(a\) white cells.
  • Therefore, \(b \leq a\).
• From the above, \(a = b\).

[The Japanese text to the left says “one repainting (★) enables movement from top-left to bottom-right only passing through red,” and the text to the right says “you can move from top-left to bottom-right passing through only one white cell.”]

The remaining challenge is how to find “how many white cells need to be passed at minimum to move from the top-left to the bottom-right.”

This can be reduced to the following shortest path problem. Please see the figure below for details.

• Treat each cell as a vertex. The number of vertices is \(N^2\).
• Treat the adjacency of cells as edges.
• The cost of an edge is \(1\) for edges leading to a white cell, and \(0\) for other edges.

Therefore, it can be solved in \(O(N^2 \log N)\) time using Dijkstra’s algorithm or similar. Since the constraint for this problem is \(N \leq 500\), it can be solved comfortably within the time limit.

[The Japanese text says “can be reduced to the shortest path problem in the graph to the right.”]

---

Sample Implementation (C++)

#include <bits/stdc++.h>
using namespace std;

const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};
int N;
int Dist[1009][1009];
char C[1009][1009];

int Solve(int sx, int sy, int gx, int gy, char target) {
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) Dist[i][j] = (1 << 30);
	}

	// BFS Init
	priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> Q;
	vector<vector<bool>> used(N + 1, vector<bool>(N + 1, false));
	Q.push(make_tuple(0, sx, sy));
	Dist[sx][sy] = 0;

	// BFS Main
	while (!Q.empty()) {
		int ax = get<1>(Q.top());
		int ay = get<2>(Q.top()); Q.pop();
		if (used[ax][ay] == true) continue;
		used[ax][ay] = true;
		for (int i = 0; i < 4; i++) {
			int bx = ax + dx[i];
			int by = ay + dy[i];
			if (bx <= 0 || by <= 0 || bx > N || by > N) continue;
			int cost = (C[bx][by] == target ? 0 : 1);
			if (Dist[bx][by] > Dist[ax][ay] + cost) {
				Dist[bx][by] = Dist[ax][ay] + cost;
				Q.push(make_tuple(Dist[bx][by], bx, by));
			}
		}
	}

	// Return
	return Dist[gx][gy];
}

int main() {
	// Step 1. Input
	cin >> N;
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) cin >> C[i][j];
	}

	// Step 2. Solve
	int Dist1 = Solve(1, 1, N, N, 'R');
	int Dist2 = Solve(1, N, N, 1, 'B');
	cout << Dist1 + Dist2 << endl;
	return 0;
}