解説 - AtCoder Regular Contest 177

コンテスト時間: 2024-05-12 21:00:00+0900 ~ 2024-05-12 23:00:00+0900 (120分) AtCoderホームへ戻る

公式

E - Wrong Scoreboard 解説 by E869120

この問題の解法

実は、コンテストの配点としては以下の \(113\) 通りしか考える必要はありません。

また、コンテストの配点が決まった場合、\(R_i\) の値が小さいほど (同点内における) ペナルティが小さくなるようにすると、二乗誤差が必ず最小となります。したがって、std::sort などを利用することで \(113N \log N\) 回程度の計算で解くことができます。

[1, 1, 1, 1, 1]
[1, 1, 1, 1, 2]
[1, 1, 1, 1, 3]
[1, 1, 1, 1, 4]
[1, 1, 1, 2, 2]
[1, 1, 1, 2, 3]
[1, 1, 1, 2, 4]
[1, 1, 1, 2, 5]
[1, 1, 1, 3, 3]
[1, 1, 1, 3, 4]
[1, 1, 1, 3, 5]
[1, 1, 1, 3, 6]
[1, 1, 2, 2, 2]
[1, 1, 2, 2, 3]
[1, 1, 2, 2, 4]
[1, 1, 2, 2, 5]
[1, 1, 2, 2, 6]
[1, 1, 2, 3, 3]
[1, 1, 2, 3, 4]
[1, 1, 2, 3, 5]
[1, 1, 2, 3, 6]
[1, 1, 2, 3, 7]
[1, 1, 2, 4, 4]
[1, 1, 2, 4, 5]
[1, 1, 2, 4, 6]
[1, 1, 2, 4, 7]
[1, 1, 2, 4, 8]
[1, 1, 3, 3, 4]
[1, 1, 3, 3, 5]
[1, 1, 3, 4, 5]
[1, 1, 3, 4, 6]
[1, 1, 3, 5, 6]
[1, 1, 3, 5, 7]
[1, 1, 4, 4, 6]
[1, 1, 4, 5, 7]
[1, 1, 4, 6, 8]
[1, 2, 2, 2, 3]
[1, 2, 2, 2, 5]
[1, 2, 2, 3, 3]
[1, 2, 2, 3, 4]
[1, 2, 2, 3, 5]
[1, 2, 2, 3, 6]
[1, 2, 2, 3, 7]
[1, 2, 2, 3, 8]
[1, 2, 2, 4, 5]
[1, 2, 2, 4, 7]
[1, 2, 2, 5, 6]
[1, 2, 2, 5, 8]
[1, 2, 3, 3, 4]
[1, 2, 3, 3, 5]
[1, 2, 3, 3, 7]
[1, 2, 3, 4, 4]
[1, 2, 3, 4, 5]
[1, 2, 3, 4, 6]
[1, 2, 3, 4, 7]
[1, 2, 3, 4, 8]
[1, 2, 3, 4, 9]
[1, 2, 3, 4,10]
[1, 2, 3, 5, 6]
[1, 2, 3, 5, 7]
[1, 2, 3, 5, 9]
[1, 2, 3, 6, 7]
[1, 2, 3, 6, 8]
[1, 2, 3, 6,10]
[1, 2, 4, 4, 5]
[1, 2, 4, 4, 7]
[1, 2, 4, 5, 6]
[1, 2, 4, 5, 7]
[1, 2, 4, 5, 8]
[1, 2, 4, 6, 7] 
[1, 2, 4, 6, 9]
[1, 2, 4, 7, 8]
[1, 2, 4, 7,10]
[1, 2, 5, 6, 8]
[1, 2, 5, 6, 9]
[1, 2, 6, 7,10]
[1, 3, 3, 4, 5]
[1, 3, 3, 5, 7]
[1, 3, 4, 4, 6]
[1, 3, 4, 5, 6]
[1, 3, 4, 5, 7]
[1, 3, 4, 6, 8]
[1, 3, 4, 7, 9]
[1, 3, 4, 8,10]
[1, 3, 5, 6, 7]
[1, 3, 5, 7, 9]
[1, 3, 6, 8,10]
[1, 4, 5, 6, 8]
[2, 2, 2, 3, 3]
[2, 2, 3, 3, 4]
[2, 2, 3, 4, 5]
[2, 2, 3, 5, 6]
[2, 2, 3, 6, 7]
[2, 2, 3, 7, 8]
[2, 3, 3, 4, 4]
[2, 3, 3, 4, 5]
[2, 3, 3, 4, 8]
[2, 3, 4, 4, 5]
[2, 3, 4, 5, 6]
[2, 3, 4, 5, 8]
[2, 3, 4, 6, 7]
[2, 3, 4, 7, 8]
[2, 3, 4, 8, 9]
[2, 3, 4, 9,10]
[2, 3, 5, 6, 7]
[2, 3, 6, 7, 8]
[2, 4, 5, 6, 7]
[2, 4, 5, 7, 8]
[2, 5, 6, 8, 9]
[3, 4, 4, 5, 6]
[3, 4, 5, 6, 7]
[3, 4, 5, 6, 8]
[4, 5, 6, 7, 8]

どうやって解法を思いつくか？

それでは、どうやって上記の解法を思い付けばよいのでしょうか。解説の後半では証明を兼ねて、解法の思い付き方について記したいと思います。

ステップ 1

まず、コンテストの配点としてどのようなものを調べれば良いのかを、以下の具体例で考えてみましょう。

コンテストの問題数は \(3\) 問である。
選手 \(1\) は問 \(1\) を解いた。
選手 \(2\) は問 \(3\) を解いた。
選手 \(3\) は問 \(1\) と問 \(2\) を解いた。

\(1\) 問目、\(2\) 問目、\(3\) 問目の配点をそれぞれ \(x_1, x_2, x_3\) とします。このとき、\(x_1, x_2, x_3\) を動かしていくと、以下のタイミングで選手の順位が入れ替わります。

\(x_3 = x_1\) のとき：選手 \(1\) と \(2\) の順位が入れ替わる
\(x_3 = x_1 + x_2\) のとき：選手 \(2\) と \(3\) の順位が入れ替わる

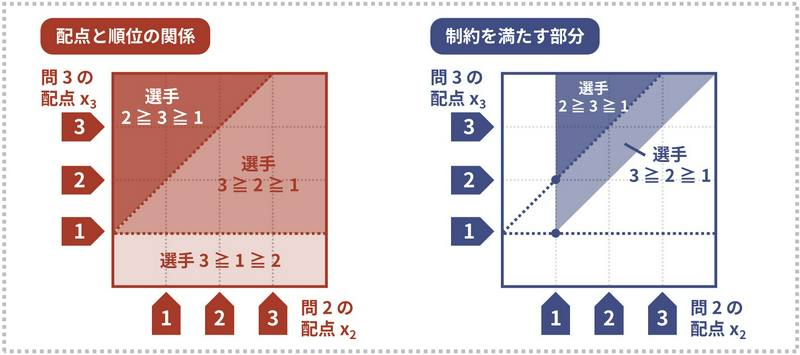
したがって、\(1\) 問目の配点が \(1\) 点であると仮定したとき、配点と順位の関係は下図左のようにして表すことができます。また、問題文をよく読むと、配点は広義単調増加 \((x_1 \leq x_2 \leq x_3)\) という制約があります。したがって、配点と順位の関係のうち制約を満たす部分は、下図右のようになります。

ここで、同点になっている選手間の順位は自由に入れ替えることができるため、コンテストの配点としては領域の境界の部分、特に交点となっている部分しか調べる必要がありません。したがって、前述の例の場合、以下の \(2\) 通りの配点しか調べる必要はありません。

\((x_1, x_2, x_3) = (1, 1, 1)\)
\((x_1, x_2, x_3) = (1, 1, 2)\)

ステップ 2

前述の考察は、コンテストの問題数が \(5\) 問の場合でも通用します。具体的には、\(2\) 人の選手の順位が入れ替わるタイミング、および制約条件 \((1 =) \ x_1 \leq x_2 \leq x_3 \leq x_4 \leq x_5\) はいくつかの \(5\) 次元空間上の超平面として表すことができますが、この中の \(4\) つの超平面が交わる点のみを配点として考えれば良いです。ステップ 1 と同様 \(x_1 = 1\) を仮定していることに注意してください。

ここで、超平面は全部でいくつあるのでしょうか。出てくる超平面は必ず \(a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4 + a_5x_5 = 0\) という形の式で表されますが、\(a_1, a_2, a_3, a_4, a_5\) の値は \(-1, 0, +1\) のうちどれかです。したがって、超平面は高々 \(3^5 = 243\) 個しか考える必要がありません。実際には、係数がすべてゼロのもの、正負を反転して同じになるものを考える必要はないので、\(121\) 個しか考える必要はありません。

したがって、配点として考えるべきものは、高々 \(C(121, 4) = 8495410\) 通りまで絞られました。

ステップ 3

ステップ 2 までの考察で、\(8495410 N \log N\) 回程度の計算で本問題を解くことが出来ました。しかし、本問題の制約は \(N \leq 3 \times 10^5\) であるため、残念ながら TLE となってしまいます。そこで次のような発想を使いましょう。

\(8495410\) 通りのうち「全く同じ配点」がたくさんあるのではないか？

実際、この発想は正しく、たとえば以下の \(5\) つの「\(4\) つの超平面の交点」はすべて \((x_1, x_2, x_3, x_4, x_5) = (1, 1, 1, 1, 2)\) で同じになっています。

超平面 \(x_1 = x_2, x_2 = x_3, x_3 = x_4, x_1 + x_2 = x_5\) の交点
超平面 \(x_1 = x_2, x_2 = x_3, x_2 = x_4, x_1 + x_3 = x_5\) の交点
超平面 \(x_1 = x_2, x_1 = x_3, x_3 = x_4, x_1 + x_4 = x_5\) の交点
超平面 \(x_1 = x_3, x_2 = x_3, x_3 = x_4, x_2 + x_3 = x_5\) の交点
超平面 \(x_1 = x_3, x_2 = x_4, x_3 = x_4, x_2 + x_4 = x_5\) の交点

それでは、重複および配点が単調増加でないものを取り除くと一体何通りになるのでしょうか。以下のプログラムで調べてみると、なんと \(113\) 通りまで絞られることが分かります。制約は \(N \leq 3 \times 10^5\) なので、これで AC を獲得することができます。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 五次元の点のクラス
struct Point5D {
	double x[5];
};

// 五次元の点の比較関数 (<)
bool operator<(const Point5D& a1, const Point5D& a2) {
	for (int i = 0; i < 5; i++) {
		if (a2.x[i] - a1.x[i] > 1.0e-9) return true;
		if (a1.x[i] - a2.x[i] > 1.0e-9) return false;
	}
	return false;
}

// 五次元の点の比較関数 (=)
bool operator==(const Point5D& a1, const Point5D& a2) {
	for (int i = 0; i < 5; i++) {
		if (a2.x[i] - a1.x[i] > 1.0e-9) return false;
		if (a1.x[i] - a2.x[i] > 1.0e-9) return false;
	}
	return true;
}

// 5 つの超平面 (4 つの超平面 + 超平面 x1=1) の交点を求める関数
// ガウスの消去法を使う (日本だと大学 1 年で習う)
Point5D GetCrossPoint(vector<Point5D> Formula, vector<double> Value) {
	for (int i = 0; i < 5; i++) {
		int pivot = -1;

		// a[j][i] が 0 で無い行 j (pivot) を求める
		for (int j = i; j < 5; j++) {
			if (abs(Formula[j].x[i]) > 1e-9) { pivot = j; break; }
		}
		if (pivot == -1) return Point5D{ -1e9, -1e9, -1e9, -1e9, -1e9 };

		// 行 i と行 pivot を交換
		swap(Formula[i], Formula[pivot]);
		swap(Value[i], Value[pivot]);

		// a[j][i] (j!=i) が 0 になるように、行 j に行 i の定数倍を引く
		for (int j = 0; j < 5; j++) {
			if (j == i) continue;
			double weight = Formula[j].x[i] / Formula[i].x[i];
			for (int k = 0; k < 5; k++) Formula[j].x[k] -= Formula[i].x[k] * weight;
			Value[j] -= Value[i] * weight;
		}
	}

	// 答えを返す
	Point5D ret;
	for (int i = 0; i < 5; i++) ret.x[i] = Value[i] / Formula[i].x[i];
	return ret;
}

int main() {
	// 121 通りの超平面を列挙する
	int pow3[5] = { 1, 3, 9, 27, 81 };
	vector<Point5D> List;
	for (int i = 122; i < 243; i++) {
		Point5D X;
		for (int j = 0; j < 5; j++) X.x[j] = ((i / pow3[j]) % 3) - 1;
		List.push_back(X);
	}

	// 8495410 個の交点を列挙する
	vector<Point5D> Candidates;
	for (int i = 0; i < 121; i++) {
		for (int j = i + 1; j < 121; j++) {
			for (int k = j + 1; k < 121; k++) {
				for (int l = k + 1; l < 121; l++) {
					vector<Point5D> Formula = { List[i], List[j], List[k], List[l] };
					vector<double> Value = { 0.0, 0.0, 0.0, 0.0 };
					Formula.push_back(Point5D{ 1.0, 0.0, 0.0, 0.0, 0.0 });
					Value.push_back(1.0);
					Point5D CrossPoint = GetCrossPoint(Formula, Value);
					if (CrossPoint.x[0] == -1e9) continue;
					if (CrossPoint.x[0] > CrossPoint.x[1] + 1.0e-9) continue;
					if (CrossPoint.x[1] > CrossPoint.x[2] + 1.0e-9) continue;
					if (CrossPoint.x[2] > CrossPoint.x[3] + 1.0e-9) continue;
					if (CrossPoint.x[3] > CrossPoint.x[4] + 1.0e-9) continue;
					Candidates.push_back(CrossPoint);
				}
			}
		}
	}

	// 重複を除去する
	sort(Candidates.begin(), Candidates.end());
	Candidates.erase(unique(Candidates.begin(), Candidates.end()), Candidates.end());
	cout << "Number of Candidates = " << Candidates.size() << endl; // 113 と出力されるはず
	return 0;
}

実装例 (C++)

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 113 通りの配点の候補
vector<vector<int>> Candidates = {
	vector<int>{1, 1, 1, 1, 1}, vector<int>{1, 1, 1, 1, 2}, vector<int>{1, 1, 1, 1, 3},
	vector<int>{1, 1, 1, 1, 4}, vector<int>{1, 1, 1, 2, 2}, vector<int>{1, 1, 1, 2, 3},
	vector<int>{1, 1, 1, 2, 4}, vector<int>{1, 1, 1, 2, 5}, vector<int>{1, 1, 1, 3, 3},
	vector<int>{1, 1, 1, 3, 4}, vector<int>{1, 1, 1, 3, 5}, vector<int>{1, 1, 1, 3, 6},
	vector<int>{1, 1, 2, 2, 2}, vector<int>{1, 1, 2, 2, 3}, vector<int>{1, 1, 2, 2, 4},
	vector<int>{1, 1, 2, 2, 5}, vector<int>{1, 1, 2, 2, 6}, vector<int>{1, 1, 2, 3, 3},
	vector<int>{1, 1, 2, 3, 4}, vector<int>{1, 1, 2, 3, 5}, vector<int>{1, 1, 2, 3, 6},
	vector<int>{1, 1, 2, 3, 7}, vector<int>{1, 1, 2, 4, 4}, vector<int>{1, 1, 2, 4, 5},
	vector<int>{1, 1, 2, 4, 6}, vector<int>{1, 1, 2, 4, 7}, vector<int>{1, 1, 2, 4, 8},
	vector<int>{1, 1, 3, 3, 4}, vector<int>{1, 1, 3, 3, 5}, vector<int>{1, 1, 3, 4, 5},
	vector<int>{1, 1, 3, 4, 6}, vector<int>{1, 1, 3, 5, 6}, vector<int>{1, 1, 3, 5, 7},
	vector<int>{1, 1, 4, 4, 6}, vector<int>{1, 1, 4, 5, 7}, vector<int>{1, 1, 4, 6, 8},
	vector<int>{1, 2, 2, 2, 3}, vector<int>{1, 2, 2, 2, 5}, vector<int>{1, 2, 2, 3, 3},
	vector<int>{1, 2, 2, 3, 4}, vector<int>{1, 2, 2, 3, 5}, vector<int>{1, 2, 2, 3, 6},
	vector<int>{1, 2, 2, 3, 7}, vector<int>{1, 2, 2, 3, 8}, vector<int>{1, 2, 2, 4, 5},
	vector<int>{1, 2, 2, 4, 7}, vector<int>{1, 2, 2, 5, 6}, vector<int>{1, 2, 2, 5, 8},
	vector<int>{1, 2, 3, 3, 4}, vector<int>{1, 2, 3, 3, 5}, vector<int>{1, 2, 3, 3, 7},
	vector<int>{1, 2, 3, 4, 4}, vector<int>{1, 2, 3, 4, 5}, vector<int>{1, 2, 3, 4, 6},
	vector<int>{1, 2, 3, 4, 7}, vector<int>{1, 2, 3, 4, 8}, vector<int>{1, 2, 3, 4, 9},
	vector<int>{1, 2, 3, 4,10}, vector<int>{1, 2, 3, 5, 6}, vector<int>{1, 2, 3, 5, 7},
	vector<int>{1, 2, 3, 5, 9}, vector<int>{1, 2, 3, 6, 7}, vector<int>{1, 2, 3, 6, 8},
	vector<int>{1, 2, 3, 6,10}, vector<int>{1, 2, 4, 4, 5}, vector<int>{1, 2, 4, 4, 7},
	vector<int>{1, 2, 4, 5, 6}, vector<int>{1, 2, 4, 5, 7}, vector<int>{1, 2, 4, 5, 8},
	vector<int>{1, 2, 4, 6, 7}, vector<int>{1, 2, 4, 6, 9}, vector<int>{1, 2, 4, 7, 8},
	vector<int>{1, 2, 4, 7,10}, vector<int>{1, 2, 5, 6, 8}, vector<int>{1, 2, 5, 6, 9},
	vector<int>{1, 2, 6, 7,10}, vector<int>{1, 3, 3, 4, 5}, vector<int>{1, 3, 3, 5, 7},
	vector<int>{1, 3, 4, 4, 6}, vector<int>{1, 3, 4, 5, 6}, vector<int>{1, 3, 4, 5, 7},
	vector<int>{1, 3, 4, 6, 8}, vector<int>{1, 3, 4, 7, 9}, vector<int>{1, 3, 4, 8,10},
	vector<int>{1, 3, 5, 6, 7}, vector<int>{1, 3, 5, 7, 9}, vector<int>{1, 3, 6, 8,10},
	vector<int>{1, 4, 5, 6, 8}, vector<int>{2, 2, 2, 3, 3}, vector<int>{2, 2, 3, 3, 4},
	vector<int>{2, 2, 3, 4, 5}, vector<int>{2, 2, 3, 5, 6}, vector<int>{2, 2, 3, 6, 7},
	vector<int>{2, 2, 3, 7, 8}, vector<int>{2, 3, 3, 4, 4}, vector<int>{2, 3, 3, 4, 5},
	vector<int>{2, 3, 3, 4, 8}, vector<int>{2, 3, 4, 4, 5}, vector<int>{2, 3, 4, 5, 6},
	vector<int>{2, 3, 4, 5, 8}, vector<int>{2, 3, 4, 6, 7}, vector<int>{2, 3, 4, 7, 8},
	vector<int>{2, 3, 4, 8, 9}, vector<int>{2, 3, 4, 9,10}, vector<int>{2, 3, 5, 6, 7},
	vector<int>{2, 3, 6, 7, 8}, vector<int>{2, 4, 5, 6, 7}, vector<int>{2, 4, 5, 7, 8},
	vector<int>{2, 5, 6, 8, 9}, vector<int>{3, 4, 4, 5, 6}, vector<int>{3, 4, 5, 6, 7},
	vector<int>{3, 4, 5, 6, 8}, vector<int>{4, 5, 6, 7, 8}
};

// 配点が {Score[0], Score[1], Score[2], Score[3], Score[4]} の場合の二乗誤差を求める関数
long long GetError(int N, vector<vector<int>>& A, vector<int>& R, vector<int> Score) {
	vector<pair<int, int>> Sorted;

	// 得点の高い順 (同点の場合は R[i] の小さい順) にソート
	for (int i = 0; i < N; i++) {
		int sum = 0;
		for (int j = 0; j < 5; j++) sum += A[i][j] * Score[j];
		Sorted.push_back(make_pair(sum, -R[i]));
	}
	sort(Sorted.begin(), Sorted.end());
	reverse(Sorted.begin(), Sorted.end());

	// 二乗誤差の合計を計算
	long long Error = 0;
	for (int i = 0; i < N; i++) {
		int idx1 = -Sorted[i].second;
		int idx2 = i + 1;
		Error += 1LL * (idx1 - idx2) * (idx1 - idx2);
	}
	return Error;
}

int main() {
	int T; cin >> T;
	for (int t = 1; t <= T; t++) {
		// 入力
		int N; cin >> N;
		vector<vector<int>> A(N, vector<int>(5, 0));
		vector<int> R(N, 0);
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < 5; j++) cin >> A[i][j];
		}
		for (int i = 0; i < N; i++) cin >> R[i];

		// 113 通りの候補を全探索し、答えを求める
		long long Answer = (1LL << 60);
		for (vector<int> cand : Candidates) {
			long long ret = GetError(N, A, R, cand);
			Answer = min(Answer, ret);
		}

		// 答えを出力
		cout << Answer << endl;
	}
	return 0;
}

投稿日時:
最終更新: