ステップ 1

いきなり一般の場合を解くのは難しいので、まずは入力例 1 を手作業で解くことを考えてみましょう。

5
RBRBB
RBRRR
RRRBR
RBBRB
BBRBR

元の問題は、以下の \(2\) つの条件を同時に考える必要があり、入力例 1 の \(5 \times 5\) 程度の大きさであっても手作業ではかなり複雑で難しいです。

• 条件 1：赤と紫のみを通って、左上から右下まで移動できる
• 条件 2：青と紫のみを通って、右上から左下まで移動できる

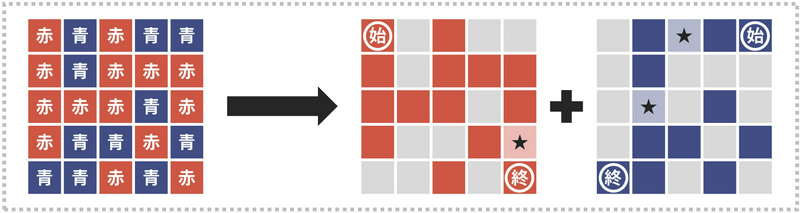
そこで、下図のようにマス目を \(2\) つに分解することを考えましょう。赤のマスは左だけが塗られている状態、青のマスは右だけが塗られている状態に対応します。また、図にはまだ表れていませんが、紫のマスは左右両方が塗られている状態に対応します。

すると、赤か青だったマスを紫にする操作は、\(2\) つのマス目のうち片方を選んで \(1\) つのマスを塗る操作に言い換えることができます。具体的には、

• 青→紫：左側のマス目の塗られてないマスを塗る
• 赤→紫：右側のマス目の塗られてないマスを塗る

にそれぞれ対応します。また、条件 1 および条件 2 は、それぞれ以下の条件に言い換えることができます。

• 条件 1：左側のマス目の塗られたマスのみを通って、左上から右下まで移動可能
• 条件 2：右側のマス目の塗られたマスのみを通って、右上から左下まで移動可能

つまり、「青→紫の操作」は条件 1 にしか影響せず、「赤→紫の操作」は条件 2 にしか影響しません。

そこで、条件 1 を満たすためには「青→紫の操作」を \(1\) 回行う必要があり (下図中央の星印)、条件 2 を満たすためには「赤→紫の操作」を \(2\) 回行う必要があるため (下図右の星印)、答えが \(1+2=3\) であると分かります。このように、\(2\) つの操作を分けて独立に考えることで、手作業でも簡単に解くことが出来ました。

---

ステップ 2

さて、ここまでは入力例 1 を解く方法について説明しましたが、一般の場合はどうやって解けばよいのでしょうか。

まず、入力例 1 と同様、マス目を \(2\) つに分解すれば赤と青を独立に考えることができるため、赤の問題を解ければ後は足し算だけで、この問題を解くことができます。つまり、赤か白で塗られているマス目が与えられるとき、最小何個のマスを赤に塗り替えれば左上から右下まで行けるようになるか、という問題を解ければ良いです。

ここで重要な性質として、最小何個のマスを赤に塗り替えれば良いかは、最小何個の白を通って左上から右下まで移動できるかと同じです。たとえば下図の場合を考えてみましょう。以下のように、確かに「\(1\)」で同じになっています。

• 最小 \(1\) 個のマスを赤に塗り替えれば、左上から右下まで移動できる
• 左上から右下まで移動するためには、最小 \(1\) 個の白マスを通る必要がある

同じになることの証明

• 左上から右下まで移動できるようにするために、赤に塗り替えるべき個数の最小値を \(a\) とする。
• 左上から右下まで行く際の、白マスを通る数の最小値を \(b\) とする。
• 次のようにして \(b \geq a\) が証明できる。
  • \(b\) 個の白マスを通る経路を考える。
  • この経路に含まれる白マスをすべて赤にすると、左上から右下まで移動できるようになる。
  • これは、\(b\) 回の塗り替えで左上から右下まで移動できるようになることを意味する。
  • したがって \(b \geq a\) となる。
• 次のようにして \(b \leq a\) が証明できる。
  • \(a\) 回の塗り替えで左上から右下まで移動できる方法について考える。
  • 塗り替え後の移動経路を \(S\) とする。
  • このとき、経路 \(S\) には元々白だったマスは高々 \(a\) 個しか含まれない。
  • これは、左上から右下まで \(a\) 回しか白マスを通らずに移動できることになる。
  • したがって \(b \leq a\) となる。
• 以上より \(a = b\) となる。

残る最後の課題は、どうやって「左上から右下まで最小何個の白マスを通って行けるか」を求めることです。

これは、次のような最短経路問題に帰着することができます。詳しくは下図をご覧ください。

• マスを頂点とする。頂点数は \(N^2\) である。
• 辺をマス目の隣接関係とする。
• 辺のコストは、白マスに向かう辺を \(1\)、そうでない辺を \(0\) とする。

したがって、ダイクストラ法などを用いて計算量 \(O(N^2 \log N)\) で解くことができます。本問題の制約は \(N \leq 500\) であるため、余裕を持って AC を得ることができます。

---

実装例 (C++)

#include <iostream>
#include <queue>
#include <tuple>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;

// dx, dy は上下左右の近傍の情報
const int dx[4] = { 1, 0, -1, 0 };
const int dy[4] = { 0, 1, 0, -1 };
int N;
int Dist[1009][1009];
char C[1009][1009];

// =============================================================== マス (sx, sy) からマス (gx, gy) まで行くのに、色 target 以外のマスを最小何個通れば良いかを求める
// =============================================================== ダイクストラ法で問題を解く
int Solve(int sx, int sy, int gx, int gy, char target) {
	// 距離の初期化
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) Dist[i][j] = (1 << 30);
	}

	// ダイクストラ法の初期化 (始点を優先度付きキューに突っ込む)
	//   - Q: 優先度付きキュー
	//   - used[i][j]: マス (i, j) の答えが既に決まったかどうか
	//   - キューには (距離, x 座標, y 座標) の組を入れる
	priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> Q;
	vector<vector<bool>> used(N + 1, vector<bool>(N + 1, false));
	Q.push(make_tuple(0, sx, sy));
	Dist[sx][sy] = 0;

	// ダイクストラ法
	while (!Q.empty()) {
		int ax = get<1>(Q.top());
		int ay = get<2>(Q.top()); Q.pop();
		if (used[ax][ay] == true) continue;
		used[ax][ay] = true;
		for (int i = 0; i < 4; i++) {
			int bx = ax + dx[i];
			int by = ay + dy[i];
			if (bx <= 0 || by <= 0 || bx > N || by > N) continue;
			int cost = (C[bx][by] == target ? 0 : 1);
			if (Dist[bx][by] > Dist[ax][ay] + cost) {
				Dist[bx][by] = Dist[ax][ay] + cost;
				Q.push(make_tuple(Dist[bx][by], bx, by));
			}
		}
	}

	// 答えを返す
	return Dist[gx][gy];
}

int main() {
	// Step 1. 入力
	cin >> N;
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) cin >> C[i][j];
	}

	// Step 2. 問題を解く
	int Dist1 = Solve(1, 1, N, N, 'R');
	int Dist2 = Solve(1, N, N, 1, 'B');

	// Step 3. 出力
	cout << Dist1 + Dist2 << endl;
	return 0;
}