Official

C - ARC Wrecker 2 Editorial by E869120

この問題も B 問題と同程度に難しく、コンテスタントの 6 割以上が苦戦しています。
しかし、最終的には典型的なテクニックを組み合わせることで解けるのです。そこで本解説では、

  • C 問題「ARC Wrecker 2」の解法と考察ステップ
  • 判定問題の答えをどう思いつくか？
  • サンプルコード

の 3 つに分けて紹介します。（急いで読みたい方は、1-4. 節のみをお読みください）


1-1. ステップ 1｜判定問題を考える

この問題を見たとき、初手すら思いつかなかった方も、読者の中には多いかもしれません。そんなときは、

  • 「判定問題」を考えてみる
  • 次に、その「判定問題」が成り立つ条件を式で表す

といった感じで考察を進めていきましょう。


ここでは、次のような判定問題を考えます。（これをあり得る全ての \((l, r)\) の組に対して考えれば、最終的な答えが分かります）

整数の組 \((l, r)\) を選んで決めたとする。
操作によって、ビル \(l, l+1, \cdots, r\) の高さをすべて \(0\) にできるか、Yes か No で答えよ。

実は、この判定問題で Yes となる必要十分条件は、次の通りになります。

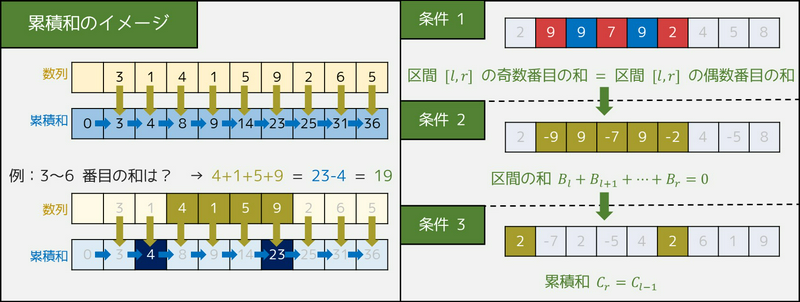
条件1
区間 \([l, r]\) において、奇数番目のビルの高さの和と、偶数番目のビルの高さの和が等しい。
つまり、\(A_l + A_{l+2} + A_{l+4} + \cdots = A_{l+1} + A_{l+3} + A_{l+5} + \cdots\) が成り立つ。

理由は「操作を行っても “偶数番目の和” と “奇数番目の和” の差が変わらないから」と考えると、理解しやすいと思います。

※この発想に至るのは結構難しいですが、適切な考察ステップを踏むと分かります。詳しくは 2 章で解説します。


1-2. ステップ 2｜条件をシンプルな形に言い換える

ステップ 1 では \((l, r)\) が決まった後の「判定問題」を条件式で表しましたが、残念ながらこの形のままだと高速に計算処理しにくいです。そこで、

  • 条件をできるだけシンプルな形に言い換える

という典型テクニックを使いましょう。


この問題では、条件1を次のように言い換えると、単純な区間和の形になります。

条件2
次のように数列 \(B = (B_1, B_2, \cdots, B_N)\) を定義することを考える。

  • \(i\) が奇数の時、\(B_i = A_i\)
  • \(i\) が偶数の時、\(B_i = -A_i\)

そのとき、条件1 は「\(B_l + B_{l+1} + \cdots + B_r = 0\)」と同値である。

また、次のように累積和を使うと、条件をさらにシンプルにすることができます。

条件3
\(C_i = B_1 + B_2 + \cdots + B_i\) とする。
そのとき、条件2 は「\(C_{r} - C_{l-1} = 0\)」、つまり「\(C_r = C_{l-1}\)」と同値である。

そうすると、C 問題「ARC Wrecker 2」は以下の問題に帰着できます。かなり単純になりましたね。

単純な問題
数列 \(C = (C_0, C_1, C_2, \cdots, C_N)\) がある。
\(C_i = C_j\) となるような \((i, j)\) \([0 \leq i < j \leq N]\) の組はいくつ存在するか？

ここまでの解法の流れのまとめは、下図の通りです。


1-3. ステップ 3｜\(O(N \log N)\) 解法

最後に、「単純な問題」はどうやって解けば良いのでしょうか。まずは簡単のため、\(0 \leq C_i \leq 10^6\) が保証されている場合を考えてみましょう。

これは次のようなアルゴリズムによって、比較的簡単に解くことができます。

やりたいこと
\(j = 1, 2, \cdots, N\) それぞれについて、\(0 \leq i \leq j-1\) かつ \(C_i = C_j\) となる個数 \(P_i\) が分かれば良い
そのとき、最終的な答えは \(P_1 + P_2 + \cdots + P_N\)

アルゴリズム
まず、配列 \(D[0], D[1], D[2], \cdots, D[10^6]\)（すべて初期値は \(0\)）を用意する。
次に、\(j = 0, 1, 2, \cdots, N\) の順に次の操作を行う。

  • \((j \geq 1\) の場合\()\) 求める \(P_j\) の値は \(D[C_j]\) であるため、それを答えに加算する
  • 配列 \(D[C_j]\) に \(1\) を加算する

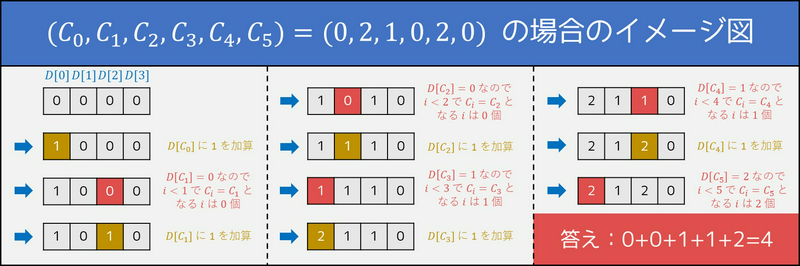
アルゴリズムのイメージは、下図のような感じです。（ここでは \(D[3]\) までしか定義されていませんが、実際は \(D[10^6]\) まで考えます）

では、\(-10^{14} \leq C_i \leq 10^{14}\) の場合はどうやって解くのでしょうか。

残念ながら、大きさ \(10^{14}\) の配列を定義すると、AtCoder ではメモリ制限超過（MLE）を起こしてしまいます。そこで、

  • std::map などの、番地が大きくても対応できる配列を使う
  • 最初に座標圧縮を行うことで \(0 \leq C_i \leq N-1\) にした上で、前述のアルゴリズムを実行する

などの対処法を使うことで、正解（AC）を出すことができるのです。詳しくは 3 章の「サンプルコード」をご覧ください。


1-4. まとめ

解法をまとめると、次のような手順で問題を解くことができます。

ステップ1　整数 \((l, r)\) を選んだときに全部高さ \(0\) にできる条件は「区間 \([l, r]\) において (奇数番目ビルの高さの和) = (偶数番目ビルの高さの和) である」
ステップ2　\(C_i = A_1 - A_2 + A_3 - A_4 + \cdots + A_i\) とすると、\(C_i = C_j\) を満たす組 \((i, j)\) \([0 \leq i < j \leq N]\) の個数を求める問題に帰着できる
ステップ3　これは std::map あるいは座標圧縮を使うことで \(O(N \log N)\) で解ける

また本問題では、「累積和などを使って条件式をシンプルにする」という考察が重要でしたが、このテクニックにより

などの問題も解くことができます。


2. 判定問題（1-1. 節）の条件はどう思いつくか？

1 章では C 問題「ARC Wrecker 2」の解法を紹介しましたが、その中でも特に、1-1. 節の「判定問題」で Yes となる条件が

(奇数番目の和) = (偶数番目の和)

であることに気づくのは難しいと思います。

そこで本章では、「どうやってそれを思いつくか？」という疑問を 2 つのアプローチで解決したいと思います。


2-1. 操作の途中過程を式で表す

まず、以下の制約を外した場合を考えてみましょう。（この制約があっても、結局は「ビルの高さを \(1\) 増やす」操作を全部行った後「ビルの高さを \(1\) 減らす」操作を行えばよいので、問題ありません）

操作中常にビルの高さが \(0\) 以上である必要がある

そのとき、どんな順番で操作しても良いので、例えば「ビル \(1, 2\) の高さを変更する」「ビル \(2, 3\) の高さを変更する」…といった順序で操作を行うことも可能です。

そこで、最終的に全ビルの高さを \(0\) にできる条件は一体何なのでしょうか。簡単のため、\(N=5\) の場合について調べてみましょう。

  • 最初のビルの高さは \((A_1, A_2, A_3, A_4, A_5)\)
  • ビル \(1\) の高さを \(0\) にするためには「ビル \(1, 2\) の高さを \(1\) 下げる」操作を \(A_1\) 回行う必要がある。操作後のビルの高さは \((0, A_2 - A_1, A_3, A_4, A_5)\)
  • ビル \(2\) の高さを \(0\) にするためには「ビル \(2, 3\) の高さを \(1\) 下げる」操作を \(A_2 - A_1\) 回行う必要がある。操作後のビルの高さは \((0, 0, A_3 - A_2 + A_1, A_4, A_5)\)
  • ビル \(3\) の高さを \(0\) にするためには「ビル \(3, 4\) の高さを \(1\) 下げる」操作を \(A_3 - A_2 + A_1\) 回行う必要がある。操作後のビルの高さは \((0, 0, 0, A_4 - A_3 + A_2 - A_1, A_5)\)
  • ビル \(4\) の高さを \(0\) にするためには「ビル \(4, 5\) の高さを \(1\) 下げる」操作を \(A_4 - A_3 + A_2 - A_1\) 回行う必要がある。操作後のビルの高さは \((0, 0, 0, A_5 - A_4 + A_3 - A_2 + A_1)\)
  • 「ビル \(5, 6\) の高さを同時に変える」という操作は存在しない

したがって、すべてのビルの高さを \(0\) にするためには、次の条件を満たす必要があると分かります。

\(A_5 - A_4 + A_3 - A_2 + A_1 = 0\) である

これを一般の \(N\) の場合にも拡張して考えると、

\(A_N - A_{N-1} + A_{N-2} - A_{N-3} + \cdots = 0\) であることが条件なのではないか？？？

と思いつくわけです。


2-2. 11 の倍数の性質に着目する

まず、\(A_1 A_2 A_3 A_4 \cdots A_N\) を十進整数 \(T\) だとみなして考えましょう。例えば

  • \((A_1, A_2, A_3, A_4) = (1, 3, 4, 2)\) の場合、\(T = 1342\)
  • \((A_1, A_2, A_3, A_4) = (3, 1, 4, 1, 5)\) の場合、\(T = 31415\)

となります。（\(A_i \geq 10\) だと不都合が起きますが、考察ステップの一段階でしかないので、\(A_i\) が小さい場合を考えます）

そこで、操作を行うと \(T\) の値はどう変化するのでしょうか。例えば \(N=4\) の場合、

  • \(A_1, A_2\) を \(1\) 増やすと \(T\) の値が \(1100\) 増える
  • \(A_1, A_2\) を \(1\) 減らすと \(T\) の値が \(1100\) 減る
  • \(A_2, A_3\) を \(1\) 増やすと \(T\) の値が \(110\) 増える
  • \(A_2, A_3\) を \(1\) 減らすと \(T\) の値が \(110\) 減る
  • \(A_3, A_4\) を \(1\) 増やすと \(T\) の値が \(11\) 増える
  • \(A_3, A_4\) を \(1\) 減らすと \(T\) の値が \(11\) 減る

ことから、「\(T\) が \(11\) の倍数であること」が「ビルの高さを全部 \(0\) にできる条件」と直接関わってきそうだと推測できます。

さて、倍数には次のような特殊な性質があります。（詳しくはこちらの記事を参照のこと）

  • \(2\) の倍数：下 \(1\) 桁が \(2\) の倍数である
  • \(3\) の倍数：各位の数字の和が \(3\) の倍数である
  • \(4\) の倍数：下 \(2\) 桁が \(4\) の倍数である
  • \(5\) の倍数：下 \(1\) 桁が \(5\) の倍数である
  • \(8\) の倍数：下 \(3\) 桁が \(8\) の倍数である
  • \(9\) の倍数：各位の数字の和が \(9\) の倍数である
  • \(11\) の倍数：「奇数桁目の和」と「偶数桁目の和」の差が \(11\) の倍数である

これらを覚えておくと、本問題では「偶数番目の和」と「奇数番目の和」が関わってきそうだと推測することができます。

この問題以外でも、例えば

などで同様のテクニックが使えます。


3. サンプルコード

各方針、各プログラミング言語における実装例は、次の通りです。

posted:
last update: