E - Connected? Editorial /

Time Limit: 2 sec / Memory Limit: 256 MB

配点 : 700700 点

問題文

すぬけ君は、パズルゲームで遊んでいます。 このパズルゲームでは、R×CR × C の長方形の盤面に、11 から NN までの整数が 22 つずつ書かれています。 整数 ii が書かれている座標は、(xi,1,yi,1)(x_{i,1},y_{i,1}) と (xi,2,yi,2)(x_{i,2},y_{i,2}) です。

すぬけ君の目的は、11 から NN までのすべての整数に対し、同じ整数の書かれている座標同士を曲線で結ぶことです。 このとき、曲線が長方形の外に出たり、互いに交わったりしてはいけません。

このようなことが可能かどうか判定してください。

制約

  • 1≦R,C≦1081 ≦ R,C ≦ 10^8
  • 1≦N≦1051 ≦ N ≦ 10^5
  • 0≦xi,1,xi,2≦R(1≦i≦N)0 ≦ x_{i,1},x_{i,2} ≦ R(1 ≦ i ≦ N)
  • 0≦yi,1,yi,2≦C(1≦i≦N)0 ≦ y_{i,1},y_{i,2} ≦ C(1 ≦ i ≦ N)
  • 与えられるどの 22 点も異なる
  • 入力は全て整数である

入力

入力は以下の形式で標準入力から与えられる。

RR CC NN
x1,1x_{1,1} y1,1y_{1,1} x1,2x_{1,2} y1,2y_{1,2}
:
xN,1x_{N,1} yN,1y_{N,1} xN,2x_{N,2} yN,2y_{N,2}

出力

すぬけ君が目的を達成できるなら YES を、そうでないなら NO を出力せよ。

入力例 1Copy

Copy
4 2 3
0 1 3 1
1 1 4 1
2 0 2 2

出力例 1Copy

Copy
YES

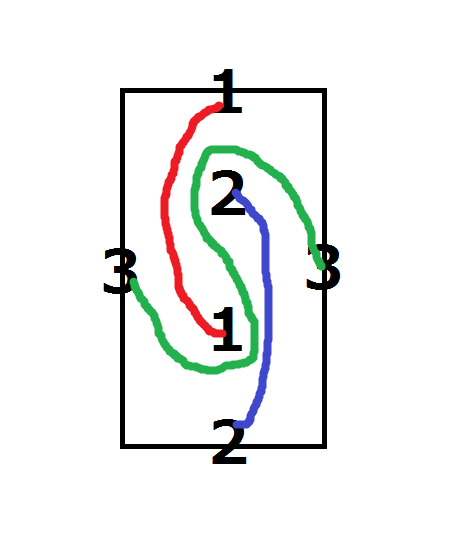
上図のように整数同士を結べば、目的を達成することができます。

入力例 2Copy

Copy
2 2 4
0 0 2 2
2 0 0 1
0 2 1 2
1 1 2 1

出力例 2Copy

Copy
NO

入力例 3Copy

Copy
5 5 7
0 0 2 4
2 3 4 5
3 5 5 2
5 5 5 4
0 3 5 1
2 2 4 4
0 5 4 1

出力例 3Copy

Copy
YES

入力例 4Copy

Copy
1 1 2
0 0 1 1
1 0 0 1

出力例 4Copy

Copy
NO

Score : 700700 points

Problem Statement

Snuke is playing a puzzle game. In this game, you are given a rectangular board of dimensions R×CR × C, filled with numbers. Each integer ii from 11 through NN is written twice, at the coordinates (xi,1,yi,1)(x_{i,1},y_{i,1}) and (xi,2,yi,2)(x_{i,2},y_{i,2}).

The objective is to draw a curve connecting the pair of points where the same integer is written, for every integer from 11 through NN. Here, the curves may not go outside the board or cross each other.

Determine whether this is possible.

Constraints

  • 1≤R,C≤1081 ≤ R,C ≤ 10^8
  • 1≤N≤1051 ≤ N ≤ 10^5
  • 0≤xi,1,xi,2≤R(1≤i≤N)0 ≤ x_{i,1},x_{i,2} ≤ R(1 ≤ i ≤ N)
  • 0≤yi,1,yi,2≤C(1≤i≤N)0 ≤ y_{i,1},y_{i,2} ≤ C(1 ≤ i ≤ N)
  • All given points are distinct.
  • All input values are integers.

Input

Input is given from Standard Input in the following format:

RR CC NN
x1,1x_{1,1} y1,1y_{1,1} x1,2x_{1,2} y1,2y_{1,2}
:
xN,1x_{N,1} yN,1y_{N,1} xN,2x_{N,2} yN,2y_{N,2}

Output

Print YES if the objective is achievable; print NO otherwise.

Sample Input 1Copy

Copy
4 2 3
0 1 3 1
1 1 4 1
2 0 2 2

Sample Output 1Copy

Copy
YES

The above figure shows a possible solution.

Sample Input 2Copy

Copy
2 2 4
0 0 2 2
2 0 0 1
0 2 1 2
1 1 2 1

Sample Output 2Copy

Copy
NO

Sample Input 3Copy

Copy
5 5 7
0 0 2 4
2 3 4 5
3 5 5 2
5 5 5 4
0 3 5 1
2 2 4 4
0 5 4 1

Sample Output 3Copy

Copy
YES

Sample Input 4Copy

Copy
1 1 2
0 0 1 1
1 0 0 1

Sample Output 4Copy

Copy
NO

2025-04-17 (Thu)
14:55:46 +00:00