 /
/ 
Time Limit: 4 sec / Memory Limit: 256 MiB
配点 : 1600 点
問題文
xy 平面上に、左下の頂点の座標が (0, 0)、右上の頂点の座標が (W, H) で、各辺が x 軸か y 軸に平行な長方形があります。最初、長方形の内部は白く塗られています。
すぬけ君はこの長方形の中に N 個の点を打ちました。i 個目 (1 ≦ i ≦ N) の点の座標は (x_i, y_i) でした。
すぬけ君は各 1 ≦ i ≦ N に対し、長方形の
- x < x_i をみたす領域
- x > x_i をみたす領域
- y < y_i をみたす領域
- y > y_i をみたす領域
の 4 つの中から 1 つを選び、その領域を黒く塗ります。
塗りつぶしが終わったあとに残る白い長方形の周長を最大化するように塗る領域を選ぶとき、その最大の周長を求めてください。
制約
- 1 ≦ W, H ≦ 10^8
- 1 ≦ N ≦ 3 \times 10^5
- 0 ≦ x_i ≦ W (1 ≦ i ≦ N)
- 0 ≦ y_i ≦ H (1 ≦ i ≦ N)
- W, H (21:32 追記), x_i, y_i は整数である
- i ≠ j ならば x_i ≠ x_j かつ y_i ≠ y_j である
入力
入力は以下の形式で標準入力から与えられる。
W H N x_1 y_1 x_2 y_2 : x_N y_N
出力
塗りつぶしが終わったあとに残る白い長方形の周長の最大値を出力せよ。
入力例 1
10 10 4 1 6 4 1 6 9 9 4
出力例 1
32
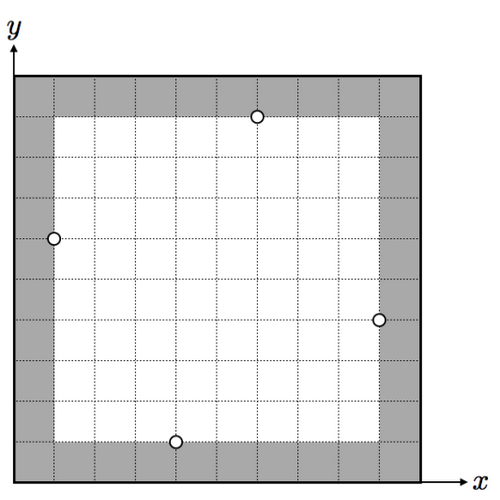
このケースでは、すぬけ君は以下の図のように長方形を塗りつぶすと残った白い長方形の周長が 32 となり、これが最大値である。
入力例 2
5 4 5 0 0 1 1 2 2 4 3 5 4
出力例 2
12
入力例 3
100 100 8 19 33 8 10 52 18 94 2 81 36 88 95 67 83 20 71
出力例 3
270
入力例 4
100000000 100000000 1 3 4
出力例 4
399999994
Score : 1600 points
Problem Statement
There is a rectangle in the xy-plane, with its lower left corner at (0, 0) and its upper right corner at (W, H). Each of its sides is parallel to the x-axis or y-axis. Initially, the whole region within the rectangle is painted white.
Snuke plotted N points into the rectangle. The coordinate of the i-th (1 ≦ i ≦ N) point was (x_i, y_i).
Then, for each 1 ≦ i ≦ N, he will paint one of the following four regions black:
- the region satisfying x < x_i within the rectangle
- the region satisfying x > x_i within the rectangle
- the region satisfying y < y_i within the rectangle
- the region satisfying y > y_i within the rectangle
Find the longest possible perimeter of the white region of a rectangular shape within the rectangle after he finishes painting.
Constraints
- 1 ≦ W, H ≦ 10^8
- 1 ≦ N ≦ 3 \times 10^5
- 0 ≦ x_i ≦ W (1 ≦ i ≦ N)
- 0 ≦ y_i ≦ H (1 ≦ i ≦ N)
- W, H (21:32, added), x_i and y_i are integers.
- If i ≠ j, then x_i ≠ x_j and y_i ≠ y_j.
Input
The input is given from Standard Input in the following format:
W H N x_1 y_1 x_2 y_2 : x_N y_N
Output
Print the longest possible perimeter of the white region of a rectangular shape within the rectangle after Snuke finishes painting.
Sample Input 1
10 10 4 1 6 4 1 6 9 9 4
Sample Output 1
32
In this case, the maximum perimeter of 32 can be obtained by painting the rectangle as follows:

Sample Input 2
5 4 5 0 0 1 1 2 2 4 3 5 4
Sample Output 2
12
Sample Input 3
100 100 8 19 33 8 10 52 18 94 2 81 36 88 95 67 83 20 71
Sample Output 3
270
Sample Input 4
100000000 100000000 1 3 4
Sample Output 4
399999994