B - 最短路問題

B - 最短路問題解説

実行時間制限: 2 sec / メモリ制限: 256 MB

高橋君は最短路アルゴリズムが大好きです。毎日さまざまな最短路アルゴリズムを実装して遊んでいます。しかし、高橋君は最短路を求めすぎてしまったので、最短路を求めるのに飽きてしまいました。

そこで高橋君は、ある頂点からほかの頂点への最短距離が特定の値になるような頂点数がNですべての辺の長さが1の無向単純グラフの数を数えることにしました。

より正確には、高橋君は同じ頂点の間を結ぶ辺が複数存在せず、またすべての辺の2端点の頂点が異なるグラフの頂点を順に1,2,...,Nとして、任意のiに対し、頂点1と頂点iを結ぶ経路上に存在する辺の個数の最小値がA_iになるようなグラフの総数を数えます。

整数NとA_1,...,A_Nが与えられるので、このようなグラフの個数を10^9+7で割った余りを求めてください。

入力は以下の形式で標準入力から与えられる。

N
A_1 A_2 ... A_N

1 行目には、グラフの頂点数N(1 ≦ N ≦ 10^5)が与えられる。
2 行目には、頂点1から頂点iまでの最短距離を表す整数列A_1,...,A_N(0 ≦ A_1,...,A_N ≦ N-1)が空白区切りで与えられる。

条件を満たすグラフの個数を10^9+7で割った余りを出力せよ。

出力の末尾に改行を入れること。(21:40修正)

4
0 1 1 2

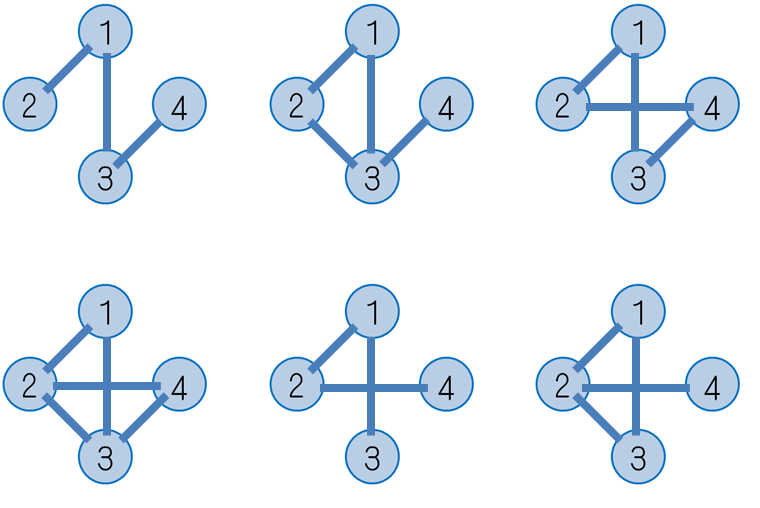
下図の6通りのグラフが条件を満たします。

4
0 1 2 0

すべての辺の長さは1なので、頂点1,4間の距離が0となるグラフはありません。

3
1 1 2

頂点1から頂点1までの距離は1にはなりえません。

17
0 1 1 2 2 4 3 2 4 5 3 3 2 1 5 4 2

855391686