B - ツリーグラフ
解説
 /
/ 
 /
/ 
実行時間制限: 2 sec / メモリ制限: 256 MiB
問題文
n 頂点から成るツリーグラフがあります.このグラフはちょうど n-1 本の辺からなり,連結であることが保障されています.このような性質を持つグラフは必ず閉路を持ちません. 各頂点番号は 1 から n の相異なる整数で表され,辺のコストは全て 1 です.
このグラフのいくつかの頂点には宝石が高々 1 つあります.宝石のある頂点にいるときのみ,その宝石を回収することができます. あなたは,とある頂点 x から出発し,全ての宝石を回収し再び頂点 x に戻ってくるような経路のうち,最短のものを求めたいと思っています.そのような経路の長さを求めなさい.経路の長さは,経路に含まれる辺のコストの総和で定義されます.
入力
入力は以下の形式で標準入力から与えられる.
n x
h_1 h_2 … h_n
a_1 b_1
a_2 b_2
:
a_{n-1} b_{n-1}
- 1 行目には,ツリーグラフの頂点の数を表す整数 n (1 ≦ n ≦ 100) と出発する頂点番号 x (1≦ x ≦n) が与えられる.
- 2 行目には,頂点 i に存在する宝石の数を表す整数 h_i (0≦h_i≦1) が n 個,スペース区切りで与えられる.
- 3 行から n-1 行,ツリーグラフの i 番目の辺が繋いでいる頂点の番号 a_i と b_i (1≦a_i,b_i≦n) が与えられる.
- 与えられるグラフに自己辺や多重辺は存在せず,連結であることが保障されている.
出力
1 行目に,求める最短経路長を出力せよ.改行を忘れないこと.
入力例1
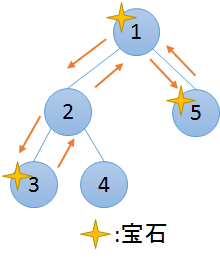
5 1 1 0 1 0 1 1 2 2 3 2 4 1 5
出力例1
6
入力のグラフと,それに対する最短経路の一例は下図の通りです.x=1 なので頂点 1 から出発しています.

入力例2
3 2 0 1 0 1 2 2 3
出力例2
0
出発地点にのみ宝石があるので,移動しないのが最短です.