B - チョコレート
Editorial
 /
/ 

 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
縦 H マス、横 W マスのチョコレートがある。各マスはブラックチョコかホワイトチョコである。ブラックチョコ同士、ホワイトチョコ同士は辺を共有しない(つまり、チョコレートは市松模様を形成している)。 各マスごとにチョコレートの濃度が定まっている。チョコレートの例を以下に表す(数字は濃度を表す)。

妹はこのチョコレートから、ある長方形領域を切り出して溶かし、チョコクリームを作成することにした。妹はチョコレートの味にこだわりを持っており、チョコクリームに使用されたブラックチョコとホワイトチョコの濃度の合計値(ただし、それぞれ使用されていない場合は濃度の合計値を 0 として扱うものとする)が等しくなければ気が済まない。
妹は条件を満たす切り出し方のうち、使用するチョコレートのマス数が最大でいくつになるのかが知りたい。
入力
入力は以下の形式で標準入力から与えられる。
H W
C_{1,1} C_{1,2} .. C_{1,W}
C_{2,1} C_{2,2} .. C_{2,W}
:
C_{H,1} C_{H,2} .. C_{H,W}
- 1 行目には、チョコレートの縦のマス数 H (1 ≦ H ≦ 100) および横のマス数 W (1 ≦ W ≦ 100) が空白区切りで与えられる。
- 2 行目から H 行では、濃度についての情報が与えられる。各行には W 個の非負整数が空白区切りで与えられる。i 行目の左から j 個目の整数 C_{i,j} (0 ≦ C_{i,j} ≦ 99) は左上隅を基準として、上から i 番目、左から j 番目のマスの濃度を表す。
出力
条件を満たす切り出し方が存在するなら、その中で使用するマス数の最大値を、存在しないなら 0 を出力せよ。出力の末尾にも改行を入れること。
入力例1
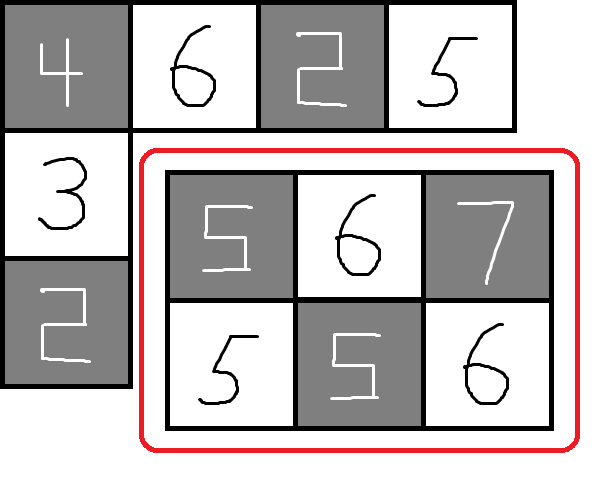
3 4 4 6 2 5 3 5 6 7 2 5 5 6
出力例1
6
下図のように縦 2 マス、横 3 マスの長方形領域を切り出せば、マス数が 6 となり、濃度の合計も 17 ずつと条件を満たす。

入力例2
2 2 4 0 7 3
出力例2
4
濃度が 0 である場合が含まれることに注意せよ。
入力例3
2 3 0 0 0 1 2 3
出力例3
3
入力例4
3 3 1 2 3 6 5 4 7 8 9
出力例4
0
この例において、条件を満たす切り出し方は存在しない。
入力例5
1 5 0 1 2 3 4
出力例5
1
ブラックチョコかホワイトチョコの一方のみを切り出す場合でも条件を満たす場合が存在することに注意せよ。