D - 切り分けできるかな？ Editorial /

Time Limit: 2 sec / Memory Limit: 64 MB

問題文

高橋君は道端に落ちていた鉄塊を切って分銅を作りたいです。
この鉄塊は特殊で、 1cm^3 で 1g であることが分かっていて、それを利用して分銅を作ります。
高橋君は心優しい青年なので、青木くんの分銅も作ってあげます。
また、高橋君は、あまり手先が器用ではないので、１つの鉄塊を切る回数を１回までとして、できるだけ多くの種類の分銅を作りたいと思いました。
鉄塊の切り方は以下の通りです。
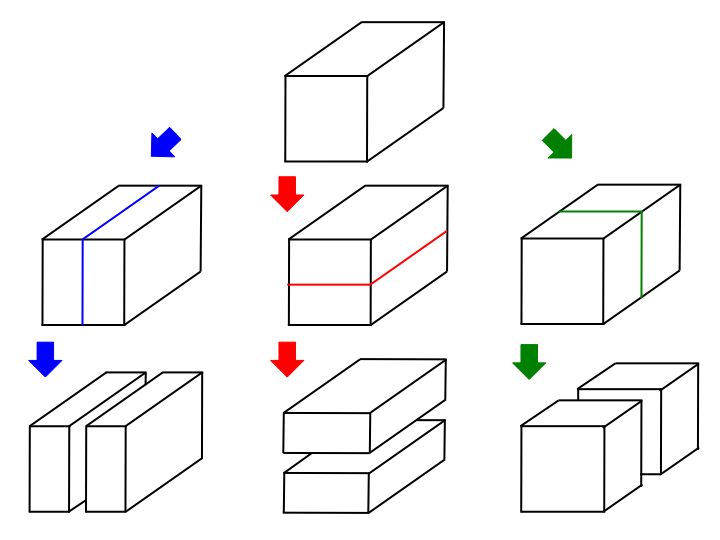
  • 鉄塊の1辺の長さが必ず整数になるように切断します。
  • 切り取り方は水平に 3 方向から切り取ることができます。つまり、斜めに切断することはできません。
  • ただし、今回はある鉄塊を切断できる回数は 1 度のみです。
  • つまり、鉄塊 A を切断して鉄塊 B と鉄塊 C を得たならば、鉄塊 B と鉄塊 C を切断することはできません。
道端に落ちていた鉄塊の種類と、それぞれのサイズが与えられるので、高橋くんの分銅と青木くんの分銅を作成するのに必要な鉄塊の数はいくつでしょうか。

入力

入力は以下の形式で標準入力から与えられる。 
N
X_{1} Y_{1} Z_{1}
X_{2} Y_{2} Z_{2}
:
X_{N} Y_{N} Z_{N}
  1. 1 行目には鉄塊の種類を示す整数 N(1≦N≦100) が与えられる。
  2. 2 行目から N+1 行までの N 行では、鉄塊の大きさが半角スペース区切りで与えられる。
    • X_{i} は i 番目の鉄塊のタテの長さ。
    • Y_{i} は i 番目の鉄塊のヨコの長さ。
    • Z_{i} は i 番目の鉄塊の高さ。
    • X_{i},Y_{i},Z_{i} はそれぞれ整数で、 1≦X_{i},Y_{i},Z_{i}≦20 であることが保証されている。

部分点

  • N = 1 を満たす入力にのみ正解した場合、部分点として 20 点が与えられる。

出力

全ての重さの分銅を作成するのに必要な鉄塊の数を 1 行で出力すること。
また、出力の最後には改行をいれること。

入力例 1

2
3 4 5
2 3 4

出力例 1

13
  • 3*4*5の鉄塊からは、3*4の面に水平に切ると、12,24,36,48
    3*5の面に水平に切ると、15,30,45
    4*5の面に水平に切ると、20,40
    と、９種類の分銅を作ることができます。
  • 2*3*4の鉄塊からは、
    2*3の面に水平に切ると、6,12,18
    2*4の面に水平に切ると、8,16
    3*4の面に水平に切ると、12
    の５種類の分銅を作ることができます。
  • これらを合わせると１３種類の分銅が存在するので、これを二人分全て揃えたいです。
  • これは、3*4*5の鉄塊9個を、(12-48) (24-36) (36-24) (48-12) (15-45) (45-15) (30-30) (20-40) (40-20)と分け、
    2*3*4の鉄塊4つを、(6-18) (18-6) (8-16) (16-8)の4つに切り分けることで、
    二人分全種類の分銅を作ることができます。

入力例 2

1
3 1 1

出力例 2

2

入力例 3

2
2 2 1
6 2 1

出力例 3

5

入力例 4

3
1 1 1
1 1 1
1 1 1

出力例 4

0