D - Shooting the Stars 解説
by  square1001
square1001
問題の言い換え 1: 区間の問題として考える
星 \(i, j\) について \(\left|X_i - X_j\right| \leq A_i + A_j\) となるのは、区間 \([X_i-A_i, X_i+A_i]\) および区間 \([X_j-A_j, X_j + A_j]\) が共通部分を持つときです(ここで区間 \([x, y]\) は座標が \(x\) 以上 \(y\) 以下の区間を表す)。
したがって、星 \(l, \dots, r\) が写るように写真を撮るとき、何個の星として写るかは、区間 \([X_l-A_l, X_l+A_l], \dots, [X_r-A_r, X_r+A_r]\) を重ねたときに何個の異なる区間として見えるか、ということになります。
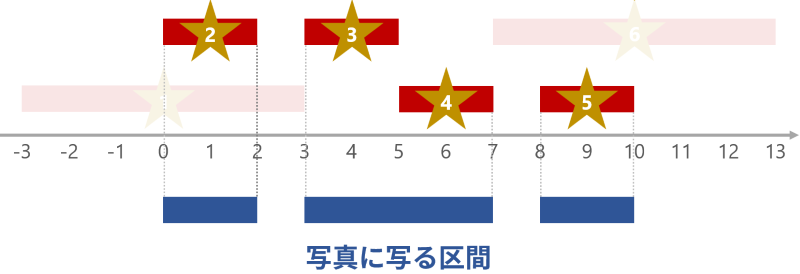
以下の図は入力例の \(2\) 番目のテストケースで、星 \(2\) から星 \(5\) までが写真に入るように撮影した場合です。区間を重ねると \(3\) つの区間として見えるので、\(3\) つの異なる星として写真に写ります。
問題の言い換え 2: 連結成分の個数は「右端の個数」
いくつの区間として見えるかどうかは、見えている右端の個数(上図でいう座標 \(2, 7, 10\))、すなわち座標 \(x\) が区間に含まれているが座標 \(x + \varepsilon\)(\(\varepsilon\) は限りなく小さい正の実数)は含まれていないような \(x\) の個数、として数えられます。
右端が見える条件は?
考えやすいように、区間の右端 \(X_1 + A_1, \dots, X_N + A_N\) はすべて異なるとします。
さて、\(X_i + A_i\) が右端として見えるような \(l, r\) の条件を考えてみましょう。まず、\(l \leq i \leq r\) となる必要があります。それに加えて、\(X_i + A_i\) をふさがないために、以下の条件が必要です(下図も参照)。
- 各 \(j \ (l \leq j < i)\) について、\(X_j + A_j < X_i + A_i\)
- 各 \(j \ (i < j \leq r)\) について、以下が成り立つ
- \(X_j < A_j\) の場合 \(X_j + A_j < X_i + A_i\)
- \(X_j \geq A_j\) の場合 \(X_j - A_j > X_i + A_i\)
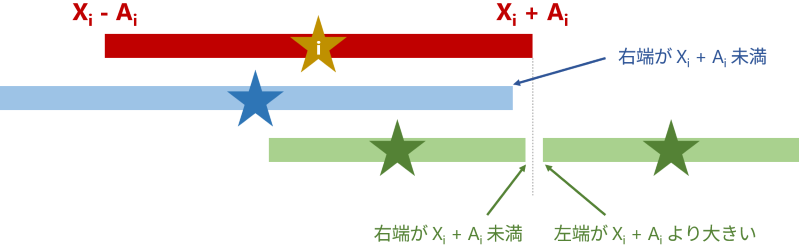
よって、1. の条件を満たさない最大の \(j\) を \(j_1\)(存在しなければ \(0\))、と 2. の条件を満たさない最小の \(j\) を \(j_2\)(存在しなければ \(N+1\))とすると、\(X_i + A_i\) が右端として見える \(l, r\) の条件は \(j_1 < l \leq i \leq r < j_2\) となります。
データ構造で高速化
ここまで準備が整ったところで、データ構造を使ってこの問題を高速に解いてみましょう。
まず、各 \(i\) に対して \(j_1, j_2\) を高速に求める必要があります。例えば \(j_1\) については、\(\max(X_j + A_j, \dots, X_{i-1} + A_{i-1}) \geq X_i + A_i\) を満たす最大の \(j\) を求めればよいので、区間最小値クエリのデータ構造(セグメント木、Sparse Table など)を使って二分探索をすれば計算量 \(O(\log N)\) で求まります。\(j_2\) についても同様です。
問題は、\(l, r\) をうまく決めたときの右端の個数の最大値を求めることです。\(X_i + A_i\) が右端として見える条件は \(j_1 < l \leq i\) かつ \(i \leq r < j_2\) なので、二次元平面上に \(l\) を X 座標、\(r\) を Y 座標として図示すると、その範囲は矩形領域(辺が X, Y 軸に平行な長方形)になります。したがって、以下の問題を解けばよいことになります。
典型問題 辺が X, Y 軸に平行な長方形が \(N\) 個与えられる。最大で何個の長方形に重なっている部分があるか?
これは実際に AtCoder 500-600 点レベルの典型問題ですので、見たことがある方も多いと思います。区間加算・区間最大値に対応する遅延評価セグメント木を使って平面走査をすると、計算量 \(O(N \log N)\) で解けます。
よって、元の問題も全体計算量 \(O(N \log N)\) で解けました。
実装例
投稿日時:
最終更新: