Considering the case \(K \geq 2\) right away is difficult, so let’s first look at the case \(K = 1\).

---

Step 1: Considering the depth diagram

First, we introduce an important concept: the depth diagram. In this diagram, each time we see an A we add \(+1\), and each time we see a C we add \(-1\), plotting the cumulative sum over the length of the string. For example, if the string is ACCAAAACAAACCCCCCCACAAAC, then its depth diagram looks like this:

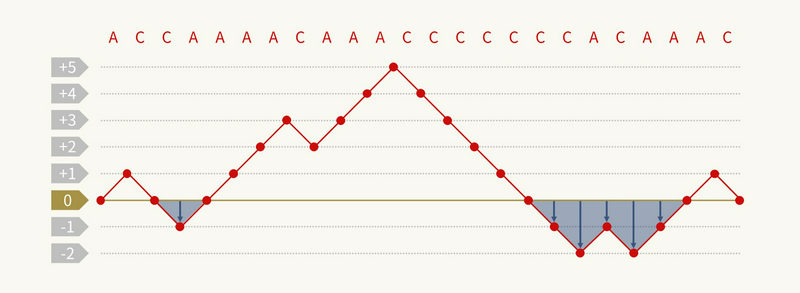
(Although not directly related to this problem, a similar diagram is often used in bracket‑sequence problems, where ( corresponds to \(+1\) and ) to \(-1\).)

Using such a diagram, we can answer: if only adjacent swaps are allowed (without the single reverse operation), how many operations are needed to turn the string into an AGC word? Clearly, if the depth never goes negative, the answer is \(0\). Otherwise, the minimum number of swaps is the sum of \(\lceil\text{negative depth}/2\rceil\), because each swap can decrease that sum by exactly \(1\).

What is \(\lceil x \rceil\)?

\(\lceil x \rceil\) is the value of \(x\) rounded up to the nearest integer. For example, \(\lceil 2025.0420 \rceil = 2026\).

Example

In the above example ACCAAAACAAACCCCCCCACAAAC, the negative depths are \(-1, -1, -2, -1, -2, -1\), and each \(\lceil\text{negative depth}/2\rceil\) equals \(1\), so the minimum number of swaps is \(6\).

If we naively try all \(O(N^2)\) choices of \((l,r)\) for the reverse, each in \(O(N)\) time to compute the swap count, we get an \(O(N^3)\) solution — too slow for \(N\le10^6\).

---

Step 2: Narrowing down the optimal \((l,r)\)

Next, we ask: when we reverse the segment \([l,r]\), how does the depth diagram change? It turns out that the segment is effectively rotated by \(180^\circ\):

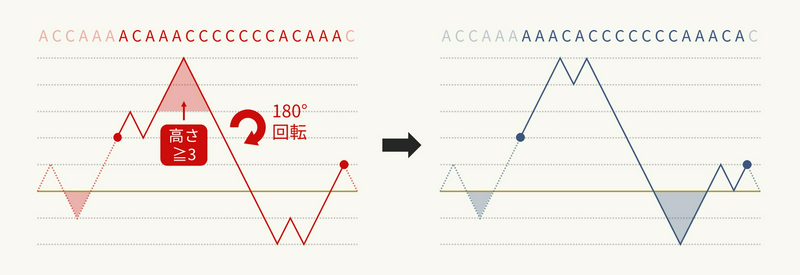
If the heights at the endpoints are \(h(l)\) and \(h(r)\), then exactly those parts of the original diagram with height at least \(h(l)+h(r)\) end up below the “waterline,” and everything else stays non‑negative. For example, in the figure above, \(h(l)=2\) and \(h(r)=1\), so only the original depths at least \(3\) end up below zero.

From this, we see that in the optimal solution neither \(h(l)\) nor \(h(r)\) can be negative.

Proof

Intuitively, a larger \(h(l)+h(r)\) is better. More precisely, if at least one of \(h(l)\) and \(h(r)\) is negative, then simultaneously doing the following will decrease the post‑reverse sum of \(\lceil\text{negative depth}/2\rceil\):

• If \(h(l)<0\), move \(l\) to the first position to the left where the depth becomes zero.
• If \(h(r)<0\), move \(r\) to the first position to the right where the depth becomes zero.

A deeper analysis shows three key properties that any optimal \((l,r)\) must satisfy (proofs follow):

• Property 1. If you split the diagram into connected components at every zero‑depth point, then \(l\) and \(r\) must each lie within the same component and be points of maximum height in that component.
• Property 2. \(l\) must be a position where the left‑to‑right maximum height is updated.
• Property 3. \(r\) must be a position where the right‑to‑left maximum height is updated.

For instance, in the example below the diagram splits into \(9\) components, of which components \(1\), \(3\), \(5\), \(7\), and \(9\) have non‑negative heights. The highest points in those components (choosing the leftmost in ties) are at positions \(1,9,17,24,32\); they satisfy Property 1. But of those, only positions \(1,9,24\) are also left‑to‑right new maxima, so \(l\) is one of \(1,9,24\).

Similarly, \(r\) is one of \(24,34\). Thus, there are only \(6\) candidates for \((l, r)\), instead of \(O(N^2)\).

The proofs of these properties all follow from the idea that (a) you want to reverse as much of the originally negative parts as possible, and (b) among those, you want to maximize \(h(l)+h(r)\).

Proof of Property 1

Suppose \(l\) is not the maximum‑height point in its zero‑delimited component, and let \(l'\) be that maximum point. Replacing \(l\) with \(l'\) cannot exclude any originally negative region nor include any region of original height \(h(l)+h(r)\) or higher, but it does increase \(h(l)+h(r)\), thus strictly decreasing (or preserving) the swap count.

Proof of Property 2

If \(l\) is not a left‑to‑right maximum, then doing the following decreases (or preserves) the swap count.

1. If position \(l-1\) is higher than position \(l\): replace \(l\) with \(l-1\).
2. If position \(l-1\) is lower than position \(l\): move \(l\) left to the first position where the depth equals its current depth.

These changes work because of the following reasons.

• For the first change, you never lose coverage of originally negative parts nor introduce new parts of height \(h(l)+h(r)\) or higher, but it increases the value of \(h(l) + h(r)\).
• For the second change, you never decrease the total height \(h(l) + h(r)\) nor introduce new parts of height \(h(l)+h(r)\) or higher, but it may introduce some originally negative region.

Proof of Property 3

Analogous to Property 2.

How many candidates for \((l, r)\) do we get?

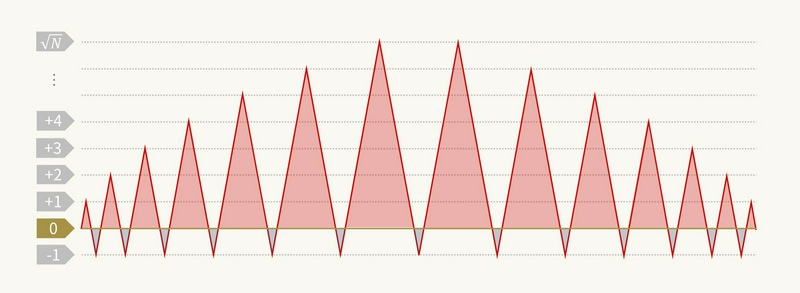
The number of left candidates \(l\) is \(O(\sqrt N)\), because the obvious worst case is the one shown in the following figure where the height changes like \(0\to1\to-1\to2\to-1\to3\to-1\to4\to\cdots\). Similarly, we have \(O(\sqrt N)\) candidates for \(r\). Thus, there are \(O(N)\) pairs, better than the previous \(O(N^2)\).

However, if we still spend \(O(N)\) time to compute the swap count for each \((l, r)\), we still take \(O(N^2)\) time. Can we speed up this computation?

---

Step 3: Speeding Up the Swap‑Count Computation

For every candidate \((l,r)\), the region of original depth \(\ge h(l)+h(r)\) is guaranteed to lie entirely within the reversed segment (by Properties 2 and 3). Therefore, the swap count is the sum of the following.

1. \(c_l\): the sum of \(\lceil\text{negative depth}/2\rceil\) for positions left of \(l\),
2. \(c_r\): the sum of \(\lceil\text{negative depth}/2\rceil\) for positions right of \(r\),
3. \(c_{\mathrm{high}}\): the sum of \(\lceil\text{negative depth}/2\rceil\) over all positions, where the height \(h(l) + h(r)\) is treated as zero, and anything higher than that is treated as negative.

Exact definition of \(c_{\mathrm{high}}\)

Let \(h(i)\) be the depth at position \(i\) \((0\le i\le2N)\). Then, \(c_{high}\) is the sum of \(\mathrm{ceil}(h(i) - (h(l) + h(r))) / 2\) over all \(0 \leq i \leq 2N\).

Each of these three values can be found in \(O(1)\) time with precomputation of prefix sums (although \(c_{\mathrm{high}}\) is slightly hard). This improves the total complexity to \(O(N)\), and we’ve finally solved the \(K=1\) case.

---

Step 4: Extending to \(K \ge 2\)

Now for the winning move. By Properties 2 and 3 again, regardless of the repeat count \(k\), the optimal \(l\) always lies in the first copy of \(S\) (the first \(2N\) characters), and \(r\) in the last copy (the last \(2N\) characters).

Now, let us fix how many characters \(l\) is from the start and how many \(r\) is from the end. Varying \(k\) simply makes the swap count \(c_l + c_r + k\,c_{\mathrm{high}}\), a linear function in \(k\).

Hence, the problem reduces to this problem: given \(O(N)\) lines \(y = a_i k + b_i\), find the minimum y-value for each \(k=1,2,\dots,K\). This can be done in \(O(N\log N + K)\) time by sorting the lines by slope. Therefore, the following implementation achieves AC.

---

Sample implementation (C++)

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const long long INF = (1LL << 60);

struct Slope {
    long long a, b; // y = a*x + b
};

// Comparison function orders by descending slope (if equal, by ascending intercept)
bool operator<(const Slope& a1, const Slope& a2) {
    if (a1.a > a2.a) return true;
    if (a1.a < a2.a) return false;
    if (a1.b < a2.b) return true;
    return false;
}

// Function to compute the minimum values at x = 1, 2, ..., K
vector<long long> get_minimum_value(int K, vector<Slope> slopes) {
    // Sort by descending slope
    sort(slopes.begin(), slopes.end());

    // Add lines one by one in descending slope order
    // current_list stores pairs of (first x-coordinate where this line is minimal, line)
    // If there are N lines, additions/removals happen O(N) times in total
    vector<pair<long long, Slope>> current_list;
    current_list.push_back(make_pair(0, Slope{INF, 0}));
    for (Slope now : slopes) {
        long long next_slope = 0;

        // Remove any lines whose minimal region vanishes due to the insertion of 'now'
        while (current_list.size() >= 1) {
            Slope pre = current_list.back().second;
            if (pre.a > now.a) {
                long long cross_point = (now.b - pre.b) / (pre.a - now.a);
                long long limit = current_list.back().first;
                if (cross_point < limit) {
                    current_list.pop_back();
                } else {
                    next_slope = cross_point + 1;
                    break;
                }
            } else {
                next_slope = INF;
                break;
            }
        }

        // Insert the current line
        if (next_slope != INF) {
            current_list.push_back(make_pair(next_slope, now));
        }
    }

    // Compute the minimum value at each x
    vector<long long> result(K + 1, 0);
    for (int i = 0; i < current_list.size(); i++) {
        long long vl = current_list[i].first;
        long long vr = (i == current_list.size() - 1 ? K + 1 : current_list[i + 1].first);
        for (long long j = max(0LL, vl); j < min(K + 1LL, vr); j++) {
            result[j] = current_list[i].second.a * j + current_list[i].second.b;
        }
    }
    return result;
}

// ------------------------------------------------------------------------------------------- Main function
int main() {
    // step 1. Input
    int N; cin >> N;
    int K; cin >> K;
    string S; cin >> S;

    // step 2. Compute the depth diagram
    vector<long long> depth(2 * N + 1, 0);
    for (int i = 0; i < 2 * N; i++) {
        depth[i + 1] = depth[i] + (S[i] == 'A' ? +1 : -1);
    }

    // step 3. Compute candidates for l
    vector<int> candidate_l = {0};
    int max_depth_l = 0;  // maximum depth
    int max_posit_l = 0;  // position of maximum depth
    for (int i = 1; i <= 2 * N; i++) {
        if (depth[i] <= 0) {
            if (candidate_l.back() != max_posit_l) {
                candidate_l.push_back(max_posit_l);
            }
        }
        if (max_depth_l < depth[i]) {
            max_depth_l = depth[i];
            max_posit_l = i;
        }
    }

    // step 4. Compute candidates for r
    vector<int> candidate_r = {2 * N};
    int max_depth_r = 0;  // maximum depth
    int max_posit_r = 0;  // position of maximum depth
    for (int i = 2 * N - 1; i >= 0; i--) {
        if (depth[i] <= 0) {
            if (candidate_r.back() != max_posit_r) {
                candidate_r.push_back(max_posit_r);
            }
        }
        if (max_depth_r < depth[i]) {
            max_depth_r = depth[i];
            max_posit_r = i;
        }
    }

    // step 5. Precompute for speeding up swap-count calculation
    vector<long long> minus_sum(2 * N + 1, 0);  // minus_sum[i]: sum of ceil(negative depth/2) up to position i
    vector<long long> highs_sum(2 * N + 1, 0);  // highs_sum[i]: sum of ceil(negative depth/2) when treating heights >= i as negative
    for (int i = 1; i <= 2 * N; i++) {
        minus_sum[i] = minus_sum[i - 1] + max(0LL, (-depth[i] + 1LL) / 2LL);
        if (depth[i] >= 1) highs_sum[depth[i] - 1] += 1;
    }

    // Take two cumulative sums to complete highs_sum
    for (int i = 2 * N - 2; i >= 0; i--) highs_sum[i] += highs_sum[i + 2];
    for (int i = 2 * N - 1; i >= 0; i--) highs_sum[i] += highs_sum[i + 1];

    // step 6. Brute-force over sqrt(N) * sqrt(N) candidate pairs to collect lines
    vector<Slope> slopes;
    for (int l : candidate_l) {
        for (int r : candidate_r) {
            long long cl = minus_sum[l];
            long long cr = minus_sum[2 * N] - minus_sum[r];
            long long chigh = highs_sum[depth[l] + depth[r]];
            slopes.push_back(Slope{chigh, cl + cr});
        }
    }

    // step 7. Compute minima of the linear functions
    vector<long long> ans = get_minimum_value(K, slopes);
    for (int i = 1; i <= K; i++) {
        cout << ans[i] << endl;
    }
    return 0;
}