B - AGC Language 解説 by E869120
いきなり \(K \geq 2\) の場合を考えると難しいので、まずは \(K = 1\) の場合を考えてみましょう。
ステップ 1: ダイヤグラムを考える
まずは重要な概念として、深さのダイヤグラムを紹介します。深さのダイヤグラムは、A が来た時に \(+1\)、C が来た時に \(-1\) をして、その経過を図で表したものを指します。たとえば文字列が ACCAAAACAAACCCCCCCACAAAC の場合、深さのダイヤグラムは下図のようになります。本問題とは直接関係ないですが、競技プログラミングではカッコ列の問題を扱うときに、( が来た時に \(+1\)、) が来た時に \(-1\) としたダイヤグラムを考えることも多いです。
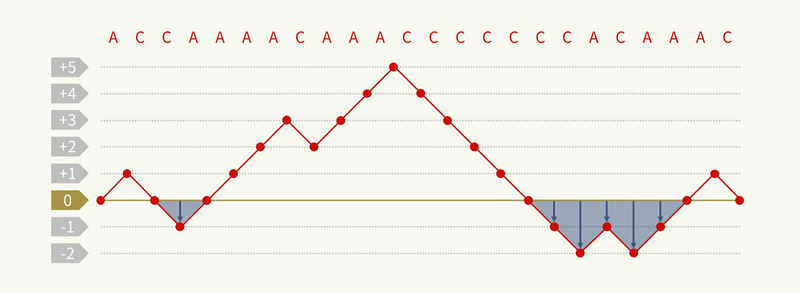
このようなダイヤグラムを使うと、もし隣接 swap しかできない場合(reverse がない場合)に何回の操作で AGC 語になるか、という問題に答えることができます。まず明らかに、高さが負になることが一度もなければ答えは \(0\) です。また、高さが負になることがある場合、負の部分における ceil(マイナスの高さ ÷ 2) の合計が最小回数になります。なぜなら、\(1\) 回の swap 操作でその値を \(1\) だけ小さくすることが出来るからです。
ceil(x) とは
x の小数点以下切り上げです。たとえば ceil(2025.0420) = 2026 です。具体例
たとえば上図の ACCAAAACAAACCCCCCCACAAAC の例の場合、マイナスの部分の高さがそれぞれ \(-1, -1, -2, -1, -2, -1\) であり ceil(マイナスの高さ ÷ 2) はすべて \(1\) なので、最小の swap 回数は \(6\) 回となります。
ここまでの考察をすると、reverse する部分 \((l, r)\) を \(O(N^2)\) 通り全探索することで、計算量 \(O(N^3)\) で解くことができます。しかし、本問題の制約は \(N \leq 10^6\) であるため、残念ながら TLE となってしまいます。
ステップ 2: 最適な操作を絞り込む
それでは、\((l, r)\) を最適な可能性があるものだけに絞り込むことで、計算量を改善することを考えてみましょう。まずは \((l, r)\) を reverse したとき、深さのダイヤグラムがどう変わるかを考えます。少し考えると、実は下図のように、reverse される部分が \(180\) 度回転されていることが分かります。
つまり、reverse 部分の左端と右端の高さをそれぞれ \(h(l), h(r)\) とするとき、元々高さが \(h(l) + h(r)\) 以上であった部分のみが水面下に沈み、それ以外の部分は水面上(つまり高さが正)になります。たとえば上図の場合、\(h(l) = 2, h(r) = 1\) なので、元々高さが \(3\) 以上である部分が水面下に沈みます。
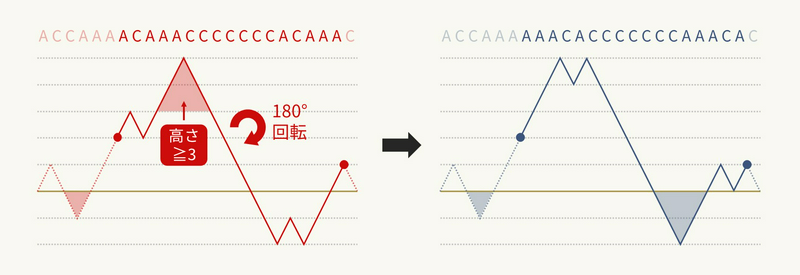
このことから、まず最適解において、\(h(l)\) と \(h(r)\) の値は絶対に負にならないことが分かります。
証明
直感的には、\(h(l) + h(r)\) が大きい方が有利であるため。正確には、もし \(h(l), h(r)\) の片方または両方が負の場合、以下の処理を同時に行うと、reverse した後の「ceil(マイナスの高さ ÷ 2) の合計」が必ず小さくなります。
さらに考察すると、以下の \(3\) つの重要な性質が成り立ちます。証明や考え方は後述します。
- 性質1 高さゼロで分かれる成分を連結成分と呼ぶ。このとき \(l, r\) は同連結成分内で高さ最大の点であるべき。
- 性質2 左端 \(l\) は左から見た時に高さの最大値が更新される位置であるべき。
- 性質3 右端 \(r\) は右から見た時に高さの最大値が更新される位置であるべき。
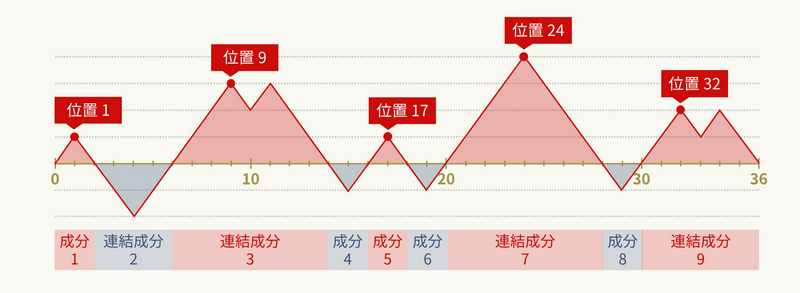
例として、下図のケースでの最適な \(l\) の候補を考えます。まず、このケースでは \(9\) 個の連結成分に分かれ、そのうち \(1, 3, 5, 7, 9\) 番目の連結成分について高さが非負です。各連結成分について、高さが最大となる点(同じ場合は最左)は位置 \(1, 9, 17, 24, 32\) であり、これら \(5\) つの点が性質 1 を満たします。しかし、位置 \(17\) および \(32\) は、左から見たときに高さの最大値を更新する点ではありません。したがって、\(l\) の候補は位置 \(1, 9, 24\) の \(3\) つに絞られます。
同様に考えると、\(r\) の候補も位置 \(24, 34\) の \(2\) つに絞られます。これで \((l, r)\) の候補が \(6\) 通りに絞られ、これまでの \(O(N^2)\) 通りと比べて大幅に減少しました。
以上 \(3\) つの性質は次のように証明することができます。ただし、直感的な証明だけであれば、元々高さが負だった部分はできるだけたくさん reverse した方が良い、それが同じであれば \(h(l) + h(r)\) の値が大きい方が良い、というアイデアを使うと簡単に示せます。
性質 1 の証明
位置 \(l\) が、同連結成分内で高さが最大の点ではないとし、同連結成分内で高さが最大となる点を \(l'\) とする。このとき、\(l\) を \(l'\) に変えると必ず swap 回数が小さくなる(か変わらない)。なぜなら、\(l\) を \(l'\) に変えても元々高さが負だった部分が reverse の範囲外になったり、高さが \(h(l) + h(r)\) 以上だった点が新しく reverse 範囲内に入ったりすることはないが、\(h(l) + h(r)\) の値が増えるため、有利になるから。性質 2 の証明
位置 \(l\) が、左から見た時に高さの最大値が更新される位置ではないとする。このとき、以下の変更をすると、必ず swap 回数が小さくなる(か変わらない)。
それぞれの変更が上手く行く理由は次のとおりである。
性質 3 の証明
性質 2 とほぼ同様に証明できる。
それでは、以上の考察で \((l, r)\) を何通りに絞ることができるのでしょうか。
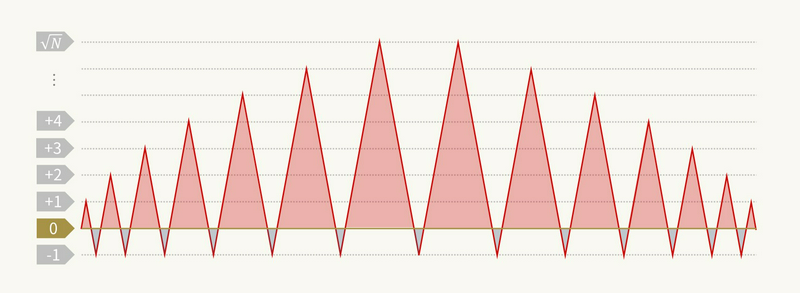
まず、\(l\) のパターン数は最悪 \(O(\sqrt{N})\) 通りです。なぜなら、下図のように高さが \(0 \to 1 \to -1 \to 2 \to -1 \to 3 \to -1 \to 4 \to -1 \to \cdots\) と変化するケースが明らかな最悪ケースだからです。同様に、\(r\) のパターン数も最悪 \(O(\sqrt{N})\) 通りです。したがって、\((l, r)\) のパターン数は最悪 \(O(\sqrt{N}) \times O(\sqrt{N}) = O(N)\) 通りとなります。これで計算量が改善されました。
しかし、もし各 \((l, r)\) について swap 回数の計算に \(O(N)\) かけた場合、計算量が \(O(N^2)\) となり、依然として TLE のままです。それでは、swap 回数の計算を高速化する方法はあるのでしょうか。
ステップ 3: swap 回数の計算の高速化
まず、探索するどの \((l, r)\) についても、高さが \(h(l) + h(r)\) 以上の点は必ず reverse 範囲内に入っています。なぜなら、どの \((l, r)\) も性質 2 と性質 3 を満たすからです。したがって、swap 回数は以下の \(3\) つの値の総和となります。
- \(c_l\): \(l\) より左の ceil(マイナスの高さ ÷ 2) の合計
- \(c_r\): \(r\) より右の ceil(マイナスの高さ ÷ 2) の合計
- \(c_{high}\): 高さ \(h(l) + h(r)\) を高さゼロ、それより上をマイナスとしたときの全体の ceil(マイナスの高さ ÷ 2) の合計
\(c_{high}\) の正確な定義
位置 \(i\) \((0 \leq i \leq 2N)\) の高さを \(h(i)\) とする。このとき \(c_{high}\) は、\(0 \leq i \leq 2N\) について \(\mathrm{ceil}(h(i) - (h(l) + h(r))) / 2\) を計算し、合計したものである。
以上の \(3\) つの値は累積和などで前計算すると計算量 \(O(1)\) で求まります(\(c_{high}\) の計算は少し難しいですが、考えてみましょう)。したがって全体の計算量は \(O(N)\) に改善され、ようやく \(K = 1\) の場合が解けました。
ステップ 4: \(K \geq 2\) への拡張
ここまで来れば、いよいよウィニングランです。まず、性質 2 および性質 3 より、繰り返し回数 \(k\) にかかわらず、\(l\) の位置は必ず最初の繰り返し(つまり最初の \(2N\) 文字)、\(r\) の位置は必ず最後の繰り返し(つまり最後の \(2N\) 文字)になることが示せます。
そこで \((l, r)\) の位置、つまり \(l\) が最初から何文字目の位置で \(r\) が最後から何文字目の位置であるかを固定し、繰り返し回数 \(k\) を動かすことを考えます。このとき、swap 回数の最小値は一次関数、具体的には \(c_l + c_r + kc_{high}\) となります。
よって、この問題は \(K\) 個の点 \(k = 1, 2, \dots, K\) について、\(O(N)\) 個の一次関数の最小値を求める問題に帰着されます。そして一次関数の最小値は、傾きでソートすることで計算量 \(O(N \log N + K)\) で計算することができます。したがって、以下の解答例のような実装をすると AC が得られます。
解答例(C++)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const long long INF = (1LL << 60);
struct Slope {
long long a, b; // y = ax + b
};
// 比較関数は傾きが大きい順 (同じ場合は y 切片が小さい順) とする
bool operator<(const Slope& a1, const Slope& a2) {
if (a1.a > a2.a) return true;
if (a1.a < a2.a) return false;
if (a1.b < a2.b) return true;
return false;
}
// x 座標が 1, 2, ..., K の時の最小値を計算する関数
vector<long long> get_minimum_value(int K, vector<Slope> slopes) {
// 傾きの大きい順にソート
sort(slopes.begin(), slopes.end());
// 傾きの大きい順に直線を 1 つずつ追加していく
// current_list には (この直線が最小となる最初の位置, 直線) のリストが入る
// 直線の数を N とすると、リストへの追加・削除はそれぞれ合計 N 回
vector<pair<long long, Slope>> current_list;
current_list.push_back(make_pair(0, Slope{ INF, 0 }));
for (Slope now : slopes) {
long long next_slope = 0;
// 今の直線を追加したことで「最小となる座標がなくなってしまった」直線を削除
while (current_list.size() >= 1) {
Slope pre = current_list[current_list.size() - 1].second;
if (pre.a > now.a) {
long long cross_point = (now.b - pre.b) / (pre.a - now.a);
long long limit = current_list[current_list.size() - 1].first;
if (cross_point < limit) {
current_list.pop_back();
}
else {
next_slope = cross_point + 1;
break;
}
}
else { next_slope = INF; break; }
}
// 今の直線を追加
if (next_slope != INF) {
current_list.push_back(make_pair(next_slope, now));
}
}
// 各点における最小値を計算
vector<long long> result(K + 1, 0);
for (int i = 0; i < current_list.size(); i++) {
long long vl = current_list[i].first;
long long vr = (i == current_list.size() - 1 ? K + 1 : current_list[i + 1].first);
for (long long j = max(0LL, vl); j < min(K + 1LL, vr); j++) {
result[j] = current_list[i].second.a * j + current_list[i].second.b;
}
}
return result;
}
// ------------------------------------------------------------------------------------------- メイン関数
int main() {
// step 1. 入力
int N; cin >> N;
int K; cin >> K;
string S; cin >> S;
// step 2. 深さのダイヤグラムを計算
vector<long long> depth(2 * N + 1, 0);
for (int i = 0; i < 2 * N; i++) {
depth[i + 1] = depth[i] + (S[i] == 'A' ? +1 : -1);
}
// step 3. L の候補を計算
vector<int> candidate_l = { 0 };
int max_depth_l = 0; // 高さの最大値
int max_posit_l = 0; // 高さが最大の位置
for (int i = 1; i <= 2 * N; i++) {
if (depth[i] <= 0) {
if (candidate_l[candidate_l.size() - 1] != max_posit_l) {
candidate_l.push_back(max_posit_l);
}
}
if (max_depth_l < depth[i]) {
max_depth_l = depth[i];
max_posit_l = i;
}
}
// step 4. R の候補を計算
vector<int> candidate_r = { 2 * N };
int max_depth_r = 0; // 高さの最大値
int max_posit_r = 0; // 高さが最大の位置
for (int i = 2 * N - 1; i >= 0; i--) {
if (depth[i] <= 0) {
if (candidate_r[candidate_r.size() - 1] != max_posit_r) {
candidate_r.push_back(max_posit_r);
}
}
if (max_depth_r < depth[i]) {
max_depth_r = depth[i];
max_posit_r = i;
}
}
// step 5. swap 回数の高速化のための前計算
vector<long long> minus_sum(2 * N + 1, 0); // minus_sum[i]: 位置 i までの「マイナス高さ / 2」の合計
vector<long long> highs_sum(2 * N + 1, 0); // minus_sum[i]: 高さ i 以上をマイナスとみなしたときの「マイナス高さ / 2」の合計
for (int i = 1; i <= 2 * N; i++) {
minus_sum[i] = minus_sum[i - 1] + max(0LL, (-depth[i] + 1LL) / 2LL);
if (depth[i] >= 1) highs_sum[depth[i] - 1] += 1;
}
// highs の計算のために 2 回累積和を取る
for (int i = 2 * N - 2; i >= 0; i--) highs_sum[i] += highs_sum[i + 2];
for (int i = 2 * N - 1; i >= 0; i--) highs_sum[i] += highs_sum[i + 1];
// step 6. sqrt(N) * sqrt(N) 通り全探索して直線の候補を得る
vector<Slope> slopes;
for (int l : candidate_l) {
for (int r : candidate_r) {
long long cl = minus_sum[l];
long long cr = minus_sum[2 * N] - minus_sum[r];
long long chigh = highs_sum[depth[l] + depth[r]];
slopes.push_back(Slope{ chigh, cl + cr });
}
}
// step 7. 一次関数の最小値を求める
vector<long long> ans = get_minimum_value(K, slopes);
for (int i = 1; i <= K; i++) {
cout << ans[i] << endl;
}
return 0;
}
投稿日時:
最終更新: