Hints → https://atcoder.jp/contests/agc063/editorial/6881

---

[1] Premises

The answer is No if there are \(i,j\) such that \(A_i = A_j\) and \(B_i\neq B_j\). We assume that there is no such \((i,j)\).

When \((A_i, B_i) = (A_j, B_j)\), it is sufficient to consider only one of \(i, j\). Thus, by properly eliminating duplicates, we can reduce the problem to the case where \(A_i\) are all distinct.

Furthermore, since the order of indices is not essential in this problem, we can reduce it to the case \(A_1 \leq \cdots \leq A_N\) by sorting. From the above, \(A_1 < \cdots < A_N\). We will assume this condition.

Since the case \(N= 1\) is simple, we will assume \(N\geq 2\). The constraint \(Y < 10^{18}\) is ignored except for the last part of the explanation.

---

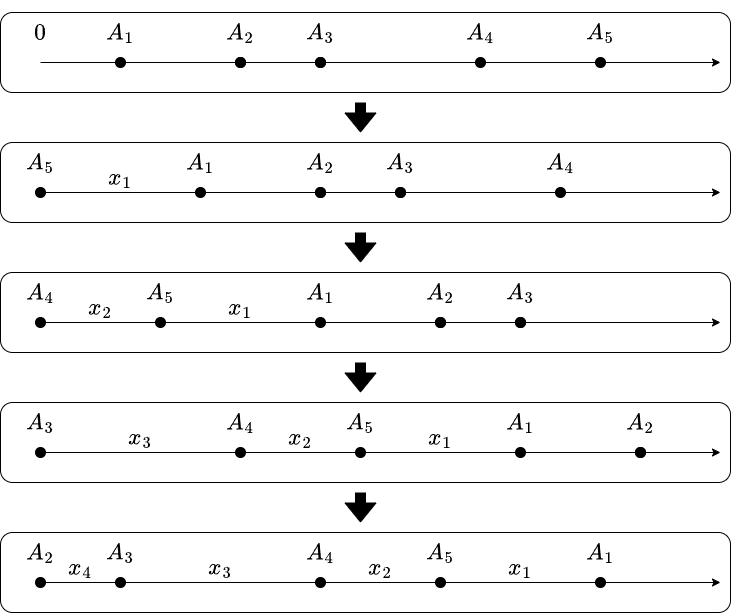
[2] Operation with \(y = x+\max(A)\)

Observe the operation with \(y = x + \max(A)\). Here, the quotient \(\lfloor A_i/y\rfloor\) is \(1\) for exactly one \(i\) and \(0\) for the other \(i\), and the division is quite simple. The following figure illustrates such an operation using a number line.

This translates all \(A_i\) and then changes the maximum value to \(0\). Note in particular the distances between two adjacent points on the number line. Then, the operation can be seen as the following action:

• delete the last “interval”, and insert a new one at the beginning.

Also, by replacing \(x\), the inserted interval can be anything at least \(A_1\), which is very flexible.

---

[3] Solution

We have seen that, if we focus on the intervals between two adjacent points on the number line, the operation in [2] is roughly equivalent to deleting the last interval and inserting a new one at the beginning. Thus, by repeating this \(N-1\) times, it seems that all intervals can be set to any value of your choice.

More precisely, the interval to be inserted at the beginning must be at least \(\min(A)\) at the time of the operation, but considering that it is \(0\) in the second and subsequent operations, the following conclusion can be drawn:

[Proposition] Suppose that a sequence of non-negative integers \((x_1, \ldots, x_{N-1})\) satisfies \(x_1\geq A_1\). Then, \(N-1\) operations can change the sequence to the following:

\[A_{2} = 0,\qquad A_{i+1} = A_i + x_{N+1-i} \, (2\leq i\leq N-1),\qquad A_1 = A_N + x_1.\]

Now, all we need to do is to choose \(x_i\) appropriately so that one operation can make \(A_i=B_i\) from this state. Here is one way to do it. Let:

\[r_i = \begin{cases}N & (i = 1) \\ i - 1 & (2\leq i\leq N)\end{cases}.\]

(After \(N-1\) operations in the manner of [Proposition], \(A_i\) will be the \(r_i\)-th point in ascending order). Let \(K\) be a sufficiently large positive integer, and let \(B_i' = B_i + Kr_i\). Then, the objective can be achieved as follows.

• \(N-1\) operations in the manner of [Proposition] can make \(A_i = B_i' - B_2\).
• Then, the \(N\)-th operation with \((x,y) = (B_2', K)\) achieves the objective.

---

Although we have neglected the constraint \(y\leq 10^{18}\) in the discussion so far, it is easy to see that \(y \leq 10^{18}\) holds for all operations under the constraint of this problem if we take \(K = 1+\max B\) and use the method described above. Thus, this problem can be solved in \(O(N)\) time.