F - Simultaneous Floor Editorial
by  maspy
maspy
ヒント → https://atcoder.jp/contests/agc063/editorial/6736
[0] 用語・記号
非負整数の \(2\) つ組を座標平面上の格子点として扱います.
\(a_1,a_2,b_1,b_2\) のいずれかが \(0\) である場合は比較的容易に解けるため,以下の解説では \(a_1,a_2,b_1,b_2\) がすべて正であることを前提とします.したがって,以下では単に「格子点」といえば,\(x,y\) 座標が正であることを仮定するものとします.
格子点 \(A\) に対して,直線 \(OA\) の傾きを単に「\(A\) の傾き」と表記します.
正の有理数 \(l,r\) (\(l<r\))に対して,傾きが \(l\) より大きく \(r\) より小さい格子点全体を \(S(l,r)\) と書くことにします.つまり
\[S(l,r) = \{(x,y)\mid x,y\in \mathbb{Z}_{>0}, l < \frac{y}{x} < r\}\]
とします.
[1] 操作回数 \(1\) 回の場合
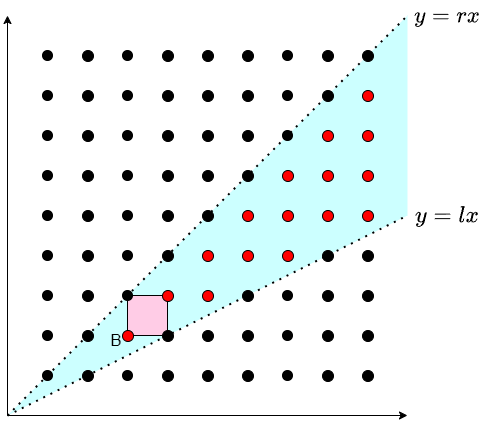
格子点 \(B(b_1,b_2)\) とします.図形的に考えると,問題の操作は次のように表すことができます:半直線 \(OA\) が正方形領域 \([b_1,b_1+1) \times [b_2,b_2+1)\) と交わるならば,\(A\) を \(B\) にうつすことができる.
逆に \(B\) を固定して考えると,\(A\) から \(B\) にうつせるような \(A\) 全体は,\(S(l,r)\) の形の集合であることが分かります.具体的には次の通りです.
【命題 1】 \(B(b_1,b_2)\) を格子点とし,\(l = \dfrac{b_2}{b_1+1}\), \(r = \dfrac{b_2+1}{b_1}\) とする.\(A\) から \(1\) 回の操作で \(B\) を得られることと,\(A\in S(l,r)\) は同値である.
[2] 操作回数 \(k\) 回の場合
格子点 \(B(b_1,b_2)\) を固定し,有理数 \(l_1, r_1\) をそれぞれ【命題 1】の \(l, r\) によって定めます.つまり \(l_1 = \dfrac{b_2}{b_1+1}\), \(r_1 = \dfrac{b_2+1}{b_1}\) とします.
\(k\geq 2\) に対して \(l_k, r_k\) を次で帰納的に定義します:
\[l_{k+1} = \min \biggl\{\frac{y}{x+1}\biggm| (x,y) \in S(l_k,r_k)\biggr\},\qquad r_{k+1} = \max \biggl\{\frac{y+1}{x}\biggm| (x,y) \in S(l_k,r_k)\biggr\}.\]
ここで \(\min\), \(\max\) が存在することは明らかではありませんが,これらの存在についてはその計算方法とともに [3] で確かめることにして,ここでは存在を認めて議論します.
直線 \(y=l_kx\) 上の格子点の隣の点を考えることで,\(l_{k+1}\leq l_k\) が分かります.同様に \(r_{k+1}\geq r_k\) も分かります.
【命題 2】 \(A\) から \(k\) 回の操作で \(B\) が得られることと,\(A\in S(l_k,r_k)\) は同値である.
\(k\) に関する帰納法で示します.次を示せばよいです:
\(A\) から \(1\) 回の操作で \(S(l_k,r_k)\) 内の点にうつせることと,\(A\in S(l_{k+1},r_{k+1})\) は同値である.
まず \(A\) が \(S(l_k,r_k)\) の点にうつせるならば \(A\in S(l_{k+1},r_{k+1})\) が成り立つことは,【命題 1】 より容易に分かります.\(A \in S(l_{k+1},r_{k+1})\) として,1 回の操作で \(A\) を \(S(l_k,r_k)\) 内の点にうつせることを示しましょう.\(A\in S(l_k,r_k)\) のときは明らかなので,\(A\) の傾きが \((l_{k+1},l_k]\) または \([r_k,r_{k+1})\) のどちらかの範囲にあるときに示せばよいです.どちらも同様なので,\(A\) の傾きが \((l_{k+1},l_k]\) の範囲 であるとします.
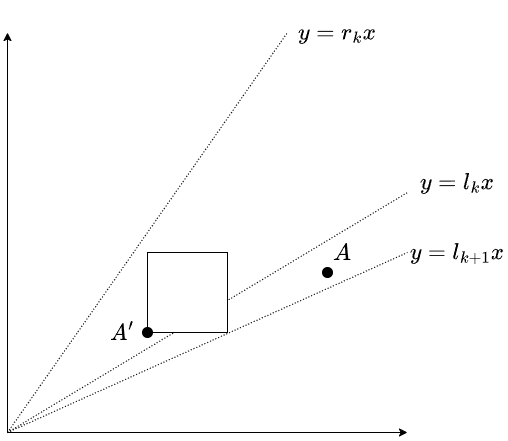
\(l_{k+1}\) の定義より,ある \(A'(x,y) \in S(l_k,r_k)\) が存在して \(l_{k+1} = \dfrac{y}{x+1}\) が成り立ちます.【命題 1】より \(S\biggl(l_{k+1},\dfrac{y+1}{x}\biggr)\) 内の点が \(A'\) にうつせる点です.\(\dfrac{y+1}{x} > \dfrac{y}{x} > l_k\) より \(A\in S\biggl(l_{k+1},\dfrac{y+1}{x}\biggr)\) なので,\(A\) を \(A'\) にうつすことができます.以上により【命題 2】が示されました.
[3] \(l_{k+1}\), \(r_{k+1}\) の計算
以下,単に「有理数 \(\dfrac{y}{x}\)」などと書けば,\(x,y\) が正整数であることを仮定します.(特に断らない限り \(\gcd(x,y)=1\) は仮定していません.)
\(l_{k+1}, r_{k+1}\) の計算方法は同様なので,\(r_{k+1}\) について解説します.
【問題】 \(l, r\) を \(l<r\) を満たす正の有理数とする.\(l<\dfrac{y}{x}<r\) を満たす有理数 \(\dfrac{y}{x}\) に対する \(\dfrac{y+1}{x}\) の最大値を求めよ.
この問題の解は,次のようになります:
\(l < \dfrac{y}{x}<r\) となる有理数 \(\dfrac{y}{x}\) のうちで,\(x\) が最小であるものをとる.ただし \(x=1\) の場合には複数の \(y\) がありうるが,この場合には \(y\) を最大にとる.このとき \(\dfrac{y+1}{x}\) が【問題】の解を与える.
このことを示しましょう.\(\dfrac{y}{x}\) を上のようにとります.\(l < \dfrac{Y}{X} < r\) を満たす有理数 \(\dfrac{Y}{X}\) に対して \(\dfrac{Y+1}{X} \leq \dfrac{y+1}{x}\) を示せばよいです.
分母 \(X\) に対する帰納法により示します.\(X=x\) のときは容易です.\(\dfrac{Y}{X}\) が \(X\geq x+1\) かつ \(l < \dfrac{Y}{X} < r\) を満たすとし,より分母の小さい有理数に対する主張を仮定します.
\(\dfrac{Y}{X}\leq \dfrac{y}{x}\) の場合は \(X(y+1)-x(Y+1)=(Xy-xY)+(X-x) > 0\) よりよいです.以下 \(\dfrac{y}{x} < \dfrac{Y}{X}\) であるとします.
\(\dfrac{Y}{X}\) が既約分数であるとして示せばよいです.分母 \(X\) までの Farey 数列において,\(\dfrac{Y}{X}\) の左隣が \(\dfrac{q}{p}\) であるとします.このとき \(\dfrac{y}{x}\leq \dfrac{q}{p}< \dfrac{Y}{X}\) です.\(x\) の最小性より \(x\leq p < X\) が成り立ちます.また Farey 数列の性質より \(pY - qX = 1\) です.
すると,\((q+1)X-p(Y+1)=(qX-pY)+X-p = X-p-1\geq 0\) より \(\dfrac{Y+1}{X} \leq \dfrac{q+1}{p}\) が成り立ちます.帰納法の仮定より \(\dfrac{q+1}{p} \leq \dfrac{y+1}{x}\) も成り立つので,\(\dfrac{Y+1}{X}\leq\dfrac{y+1}{x}\) が示されました.
[4] まとめ
結局,\(l_{k+1}, r_{k+1}\) は次のように計算できることが分かりました.
\(l_k < \dfrac{y}{x} < r_k\) となる有理数 \(\dfrac{y}{x}\) のうちで \(x\) が最小のものをとる.\(x=1\) のときはさらに \(y\) が最大のものをとる.\(r_{k+1} = \dfrac{y+1}{x}\) である.
\(l_k < \dfrac{y}{x} < r_k\) となる有理数 \(\dfrac{y}{x}\) のうちで \(y\) が最小のものをとる.\(y=1\) のときはさらに \(x\) が最大のものをとる.\(l_{k+1} = \dfrac{y}{x+1}\) である.
これらを満たす \(\dfrac{y}{x}\)は,Farey 数列(あるいは Stern-Brocot tree)の挙動を考えれば計算できます.
\(x=1\) や \(y=1\) に到達すると \(l_k=l_{k+1}\) や \(r_k=r_{k+1}\) が成り立ち,そこから先の \(l_k,r_k\) は一定になります.よって,\(l_k, r_k\) が一定になるまたは \(A\in S(l_k,r_k)\) になるまで上で述べた計算を繰り返すことにより,本問題の答えを求めることができます.
最後に,\(l_k, r_k\) が \(O(\log (b_1+b_2))\) 回で収束することを示しておきます.
\(x=1\) や \(y=1\) に到達するまでは,\(l_{k+1}, r_{k+1}\) の計算に用いられる \(\dfrac{y}{x}\) は同じ有理数です.この有理数を \(\dfrac{y_k}{x_k}\) と書けば,\(\dfrac{y_{k+1}}{x_{k+1}}\) は \(l_k=\dfrac{y_k}{x_k+1} < \dfrac{y}{x} < \dfrac{y_k+1}{x_k}=r_k\) となる有理数 \(\dfrac{y}{x}\) のうちで分母最小のものです.\(x_k,y_k,x_{k+1},y_{k+1}>1\) のときに,\(x_{k+1} \leq \dfrac{2x_k+1}{3}\) が成り立つことを示します.
分母 \(x_{k+1}\) 以下の Farey 数列における \(\dfrac{y_{k+1}}{x_{k+1}}\) の左隣・右隣を \(\dfrac{q}{p}\), \(\dfrac{s}{r}\) とします.すると \(x_k+1\geq p + x_{k+1}\), \(x_k\geq r + x_{k+1}\) が成り立つので,これらを足して \(2x_k + 1\geq p+r+2x_{k+1}\) が分かりますが,\(p+r=x_{k+1}\) なので \(3x_{k+1}\leq 2x_k+1\) となり示されました.
このことなどから,\(l_k, r_k\) が \(O(\log (b_1+b_2))\) 回で収束します.よって本問題はテストケースごとに \(O(\log^2(b_1+b_2))\) 時間で解くことができます.また,通常 \(\dfrac{y_{k+1}}{x_{k+1}}\) が Stern-Brocot tree における \(\dfrac{y_k}{x_k}\) の先祖であることを利用して,\(O(\log(b_1+b_2))\) 時間で解くこともできます.
posted:
last update: