ヒント → https://atcoder.jp/contests/agc063/editorial/6736

---

[1] 前提

\(A_i = A_j\) かつ \(B_i\neq B_j\) となる \(i,j\) があれば，答は No です．以下このような \((i,j)\) が存在しないことを仮定します．

\((A_i, B_i) = (A_j, B_j)\) であるとき，\(i, j\) のうち片方についての条件だけを考えれば十分です．よって適切に重複を取り除いて，\(A_i\) がすべて相異なる場合に帰着できます．

さらに本問題では添字の順序は本質的ではないので，ソートにより \(A_1 \leq \cdots \leq A_N\) の場合に帰着することができます．上で述べたことより \(A_1 < \cdots < A_N\) です．以下この条件を仮定します．

\(N = 1\) のときは容易なので，以下では \(N\geq 2\) を仮定します．また，解説の最後の部分を除き，\(y < 10^{18}\) という制約は無視しています．

---

[2] \(y = x+\max(A)\) の場合の操作

\(y = x + \max(A)\) とした場合の操作を観察します．このとき，商 \(\lfloor A_i/y\rfloor\) はちょうどひとつの \(i\) で \(1\)，それ以外の \(i\) で \(0\) となり，除算の様子がかなり簡潔になります．この場合の操作を数直線を用いて図示すると，次のようになります．

\(A_i\) 全体を平行移動したあと，最大値を \(0\) に変化させます．特に，数直線上で隣接する \(2\) 点の間隔に注目しましょう．すると，

• 末尾の「間隔」を削除し，先頭に新しい「間隔」を挿入する

という形になっています．また \(x\) を取り換えれば，挿入できる「間隔」は \(A_1\) 以上であれば何でもよく，非常に自由度が高いです．

---

[3] 解法

数直線上で隣接する \(2\) 点の間隔に注目すれば，[2] の操作は大雑把に見れば，「末尾の間隔を削除し先頭に新たな間隔を挿入する」という操作になっているのでした．よってこれを \(N-1\) 回繰り返せば，すべての間隔を自分で選んだ好きな値にできそうです．

より正確には，先頭に挿入する間隔は操作時点での \(\min(A)\) 以上でなくてはいけませんが，\(2\) 回目以降の操作ではこれは \(0\) であることを考えると，次の結論が得られます：

【命題】 非負整数列 \((x_1, \ldots, x_{N-1})\) が \(x_1\geq A_1\) を満たすとする．このとき，\(N-1\) 回の操作により数列を次のように変化させることができる．

\[A_{2} = 0,\qquad A_{i+1} = A_i + x_{N+1-i} \, (2\leq i\leq N-1),\qquad A_1 = A_N + x_1.\]

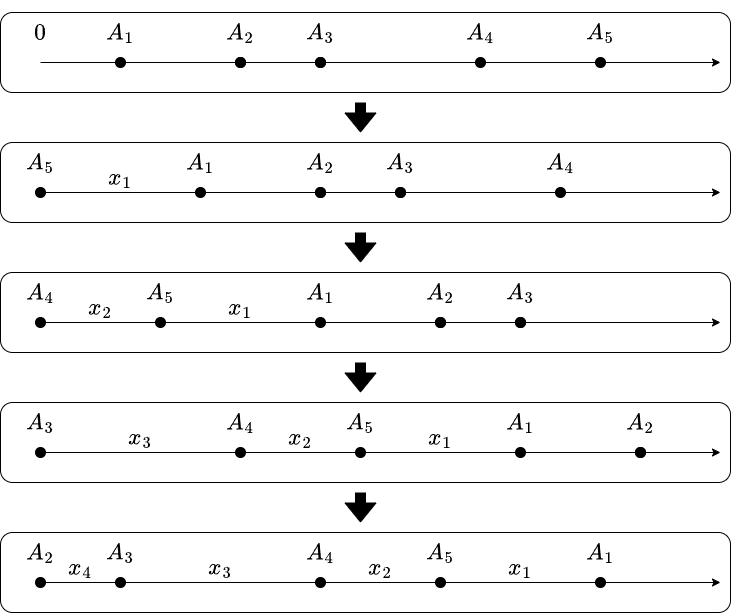
あとは \(x_i\) を適切に選ぶことで，この状態から \(1\) 回で \(A_i=B_i\) にできるようにすればよいです．例えば次のようにすればよいです．

\[r_i = \begin{cases}N & (i = 1) \\ i - 1 & (2\leq i\leq N)\end{cases}\]

とします（【命題】 の方法で，\(N-1\) 回の操作で \(A_i\) が昇順で \(r_i\) 番目に並びます）．\(K\) を十分大きな正整数とし，\(B_i' = B_i + Kr_i\) とします．このとき，

• 【命題】 の方法で，\(N-1\) 回の操作により \(A_i = B_i' - B_2\) が成り立つようにできる．
• したがって，\(N\) 回目の操作を \((x,y) = (B_2', K)\) として行うことで目的が達成できる．

のでよいです．

---

ここまでの議論で制約 \(y\leq 10^{18}\) を無視してきましたが，\(K = 1+\max B\) ととり上で述べた方法をとれば，本問題の制約のもとですべての操作で \(y \leq 10^{18}\) が成り立つことは容易に分かります．以上により，本問題は \(O(N)\) 時間で解くことができます．