 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1700 点
問題文
高橋王国には,1 本の鉄道路線が走っています. この路線は N 個の区間 1, 2, ..., N と N+1 個の駅 0, 1, ..., N からなり,区間 i は駅 i-1 と駅 i を直接結んでいます. 列車が区間 i を走行するには,方向によらず,ちょうど A_i 分かかります. また,N 個の区間のそれぞれは,区間全体にわたって複線であるか,区間全体にわたって単線であるかのどちらかです. B_i = 1 のときは区間 i は単線,B_i = 2 のときは区間 i は複線です. 複線の区間では両方向の列車がすれ違うことができますが,単線の区間ではすれ違うことはできません. ただし,列車が駅にいる場合は列車同士がすれ違うことができます.
すぬけ君は,この路線に図のように K 分間隔で列車を走らせようとしています.ここで,太線は列車が走行している位置を表します. (詳しくは,入出力例 1 を見てください.)
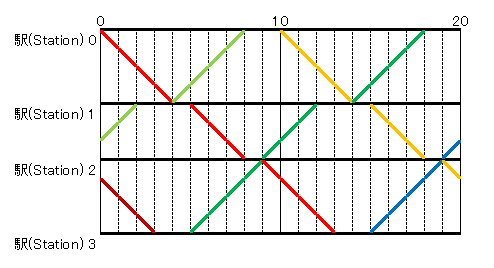
このとき,駅 0 から駅 N までの列車の所要時間と,駅 N から駅 0 までの列車の所要時間の合計の最小値を求めてください. この問題の制約の下,適切な列車の走らせ方が存在するとき,この最小値は必ず整数になることが証明できます.
なお,列車の発車時刻や到着時刻が満たすべき条件は,厳密に書くと下のようになります.
- どの列車も,駅 0 を出発して駅 N まで向かうか,駅 N を出発して駅 0 まで向かうかのいずれかである.
- どの列車も,区間 i をちょうど A_i 分かけて走行する.例えば,駅 N 行きのある列車が駅 i-1 を時刻 t に出発したなら,この列車は駅 i にちょうど時刻 t+A_i に到着する.
- ある駅で,時刻 s に駅 N 行きの列車が到着し,その列車が時刻 t に発車したとすると,駅 N 行きの次の列車は時刻 s+K に到着し,時刻 t+K に発車する.また,駅 N 行きの前の列車は時刻 s-K に到着し,時刻 t-K に発車する.駅 0 行きの列車についても同様である.
- 異なる方向の列車が,同時に同じ単線区間(両端の駅を除く)を走行していてはならない.
制約
- 1 \leq N \leq 100000
- 1 \leq K \leq 10^9
- 1 \leq A_i \leq 10^9
- A_i は整数
- B_i = 1 または B_i = 2
部分点
- 500 点分のテストケースでは,すべての区間が単線である.すなわち,B_i = 1 が成り立つ.
- 別の 500 点分のテストケースでは,N \leq 200 が成り立つ.
入力
入力は以下の形式で標準入力から与えられる。
N K A_1 B_1 A_2 B_2 : A_N B_N
出力
駅 0 から駅 N までの列車の所要時間と,駅 N から駅 0 までの列車の所要時間の合計の最小値を表す整数を出力せよ. ただし,条件をすべて満たすように列車を走らせることが不可能な場合は,-1 を出力せよ.
入力例 1
3 10 4 1 3 1 4 1
出力例 1
26
例えば,下図に示すように列車を走らせると,所要時間の合計が 26 分になります.

例えば,赤線で示した列車は,時刻 0 に駅 0 を出発し,時刻 4 に駅 1 に到着し,時刻 5 に駅 1 を出発し,時刻 8 に駅 2 に到着します.
入力例 2
1 10 10 1
出力例 2
-1
入力例 3
6 4 1 1 1 1 1 1 1 1 1 1 1 1
出力例 3
12
入力例 4
20 987654321 129662684 2 162021979 1 458437539 1 319670097 2 202863355 1 112218745 1 348732033 1 323036578 1 382398703 1 55854389 1 283445191 1 151300613 1 693338042 2 191178308 2 386707193 1 204580036 1 335134457 1 122253639 1 824646518 2 902554792 2
出力例 4
14829091348
Score : 1700 points
Problem Statement
There is a railroad in Takahashi Kingdom. The railroad consists of N sections, numbered 1, 2, ..., N, and N+1 stations, numbered 0, 1, ..., N. Section i directly connects the stations i-1 and i. A train takes exactly A_i minutes to run through section i, regardless of direction. Each of the N sections is either single-tracked over the whole length, or double-tracked over the whole length. If B_i = 1, section i is single-tracked; if B_i = 2, section i is double-tracked. Two trains running in opposite directions can cross each other on a double-tracked section, but not on a single-tracked section. Trains can also cross each other at a station.
Snuke is creating the timetable for this railroad. In this timetable, the trains on the railroad run every K minutes, as shown in the following figure. Here, bold lines represent the positions of trains running on the railroad. (See Sample 1 for clarification.)

When creating such a timetable, find the minimum sum of the amount of time required for a train to depart station 0 and reach station N, and the amount of time required for a train to depart station N and reach station 0. It can be proved that, if there exists a timetable satisfying the conditions in this problem, this minimum sum is always an integer.
Formally, the times at which trains arrive and depart must satisfy the following:
- Each train either departs station 0 and is bound for station N, or departs station N and is bound for station 0.
- Each train takes exactly A_i minutes to run through section i. For example, if a train bound for station N departs station i-1 at time t, the train arrives at station i exactly at time t+A_i.
- Assume that a train bound for station N arrives at a station at time s, and departs the station at time t. Then, the next train bound for station N arrives at the station at time s+K, and departs the station at time t+K. Additionally, the previous train bound for station N arrives at the station at time s-K, and departs the station at time t-K. This must also be true for trains bound for station 0.
- Trains running in opposite directions must not be running on the same single-tracked section (except the stations at both ends) at the same time.
Constraints
- 1 \leq N \leq 100000
- 1 \leq K \leq 10^9
- 1 \leq A_i \leq 10^9
- A_i is an integer.
- B_i is either 1 or 2.
Partial Score
- In the test set worth 500 points, all the sections are single-tracked. That is, B_i = 1.
- In the test set worth another 500 points, N \leq 200.
Input
The input is given from Standard Input in the following format:
N K A_1 B_1 A_2 B_2 : A_N B_N
Output
Print an integer representing the minimum sum of the amount of time required for a train to depart station 0 and reach station N, and the amount of time required for a train to depart station N and reach station 0. If it is impossible to create a timetable satisfying the conditions, print -1 instead.
Sample Input 1
3 10 4 1 3 1 4 1
Sample Output 1
26
For example, the sum of the amount of time in question will be 26 minutes in the following timetable:

In this timetable, the train represented by the red line departs station 0 at time 0, arrives at station 1 at time 4, departs station 1 at time 5, arrives at station 2 at time 8, and so on.
Sample Input 2
1 10 10 1
Sample Output 2
-1
Sample Input 3
6 4 1 1 1 1 1 1 1 1 1 1 1 1
Sample Output 3
12
Sample Input 4
20 987654321 129662684 2 162021979 1 458437539 1 319670097 2 202863355 1 112218745 1 348732033 1 323036578 1 382398703 1 55854389 1 283445191 1 151300613 1 693338042 2 191178308 2 386707193 1 204580036 1 335134457 1 122253639 1 824646518 2 902554792 2
Sample Output 4
14829091348