 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 675 点
問題文
2 次元座標平面に、 点 (\frac{A}{C}, \frac{B}{C}) を中心とする半径 \frac{\sqrt{N}}{C} の円があります。 この円の円周上にある格子点の個数を 998244353 で割ったあまりを求めてください。
なお、 N は N=\prod_{i=1}^{M} P_i^{E_i} と素因数分解された形で与えられます。
制約
- N \geq 1
- 2 \leq P_i \leq 100
- P_i は相異なる素数
- 1 \leq E_i \leq 10^{18}
- 1 \leq C \leq 50
- 0 \leq A,B \lt C
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
A B C M P_1 E_1 P_2 E_2 \vdots P_M E_M
出力
答えを出力せよ。
入力例 1
1 1 2 2 2 1 5 2
出力例 1
12
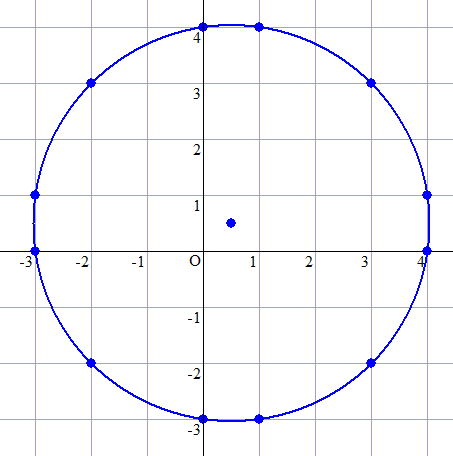
下図に示す通り、円周上に 12 個の格子点があります。
入力例 2
1 5 14 4 2 1 5 1 13 1 17 1
出力例 2
4
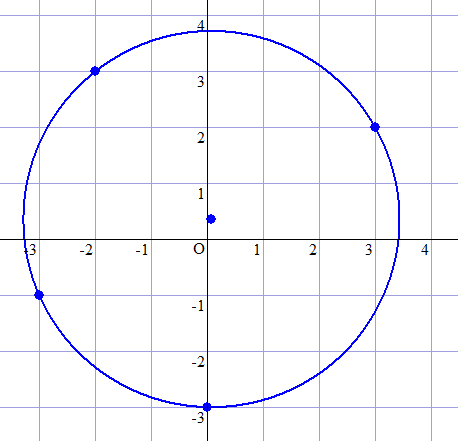
下図に示すとおり、円周上に 4 個の格子点があります。
入力例 3
1 1 6 3 2 1 5 2 13 1
出力例 3
6
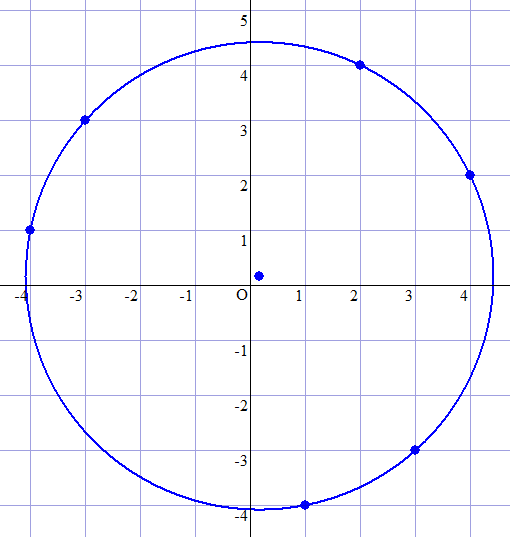
下図に示すとおり、円周上に 6 個の格子点があります。
入力例 4
0 0 1 10 97 1000000000000000000 89 1000000000000000000 73 1000000000000000000 61 1000000000000000000 59 1000000000000000000 47 1000000000000000000 31 1000000000000000000 23 1000000000000000000 11 1000000000000000000 5 1000000000000000000
出力例 4
7885876
998244353 で割った余りを求めてください。
Score : 675 points
Problem Statement
On a two-dimensional coordinate plane, there is a circle with center at point (\frac{A}{C}, \frac{B}{C}) and radius \frac{\sqrt{N}}{C}. Find the number, modulo 998244353, of lattice points on the circumference of this circle.
N is given in its prime factorization form as N=\prod_{i=1}^{M} P_i^{E_i}.
Constraints
- N \geq 1
- 2 \leq P_i \leq 100
- P_i are distinct primes.
- 1 \leq E_i \leq 10^{18}
- 1 \leq C \leq 50
- 0 \leq A,B \lt C
- All input values are integers.
Input
The input is given from Standard Input in the following format:
A B C M P_1 E_1 P_2 E_2 \vdots P_M E_M
Output
Output the answer.
Sample Input 1
1 1 2 2 2 1 5 2
Sample Output 1
12
As shown in the figure below, there are 12 lattice points on the circumference.

Sample Input 2
1 5 14 4 2 1 5 1 13 1 17 1
Sample Output 2
4
As shown in the figure below, there are 4 lattice points on the circumference.

Sample Input 3
1 1 6 3 2 1 5 2 13 1
Sample Output 3
6
As shown in the figure below, there are 6 lattice points on the circumference.

Sample Input 4
0 0 1 10 97 1000000000000000000 89 1000000000000000000 73 1000000000000000000 61 1000000000000000000 59 1000000000000000000 47 1000000000000000000 31 1000000000000000000 23 1000000000000000000 11 1000000000000000000 5 1000000000000000000
Sample Output 4
7885876
Find the number modulo 998244353.