 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
1 から N の番号がついた N 個のマスがあります。最初、どのマスも色が塗られていません。
M 種類の色があり、i 番目の色ではマス L_i,L_i+1,\ldots,R_i のうち好きなマスを好きな個数塗ることができます。
以下の条件を満たす色の塗り方は何通りあるか、998244353 で割った余りを求めてください。
- どのマス i についても、そのマスに色が塗られているならば、マス i-1,i+1 のうちちょうど一方がマス i と同じ色で塗られている。
- ただし、マス 0,N+1 はどの色にも塗られていないとみなす。
制約
- 1\leq N,M \leq 5\times 10^5
- 1\leq L_i \leq R_i \leq N
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N M L_1 R_1 \vdots L_M R_M
出力
答えを出力せよ。
入力例 1
5 2 1 3 1 5
出力例 1
11
1 番目の色ではマス 1,2,3 を、2 番目の色ではマス 1,2,3,4,5 を塗ることができます。
条件を満たす塗り方は以下の 11 通りです。
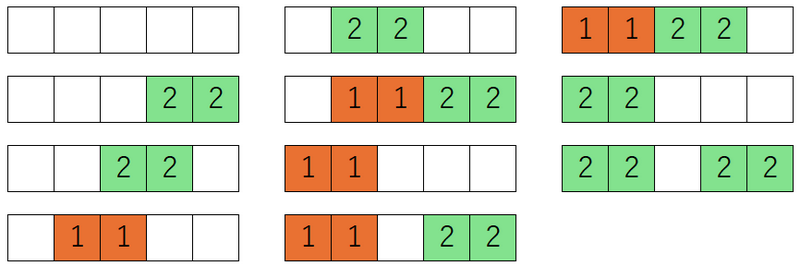
入力例 2
3 3 1 1 2 2 3 3
出力例 2
1
どのマスにも色を塗らない 1 通りが条件を満たします。
入力例 3
500000 10 1 499999 2 499998 3 499997 4 499996 5 499995 6 499994 7 499993 8 499992 9 499991 10 499990
出力例 3
775503999
998244353 で割った余りを求めてください。
Score : 600 points
Problem Statement
There are N cells numbered from 1 to N. Initially, no cell is painted with any color.
There are M types of colors, and with the i-th color, you can paint any number of cells you like among cells L_i,L_i+1,\ldots,R_i.
Find the number, modulo 998244353, of ways to paint the cells that satisfy the following condition:
- For every cell i, if that cell is painted with a color, then exactly one of cells i-1 and i+1 is painted with the same color as cell i.
- Here, cells 0 and N+1 are considered to be not painted with any color.
Constraints
- 1\leq N,M \leq 5\times 10^5
- 1\leq L_i \leq R_i \leq N
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M L_1 R_1 \vdots L_M R_M
Output
Output the answer.
Sample Input 1
5 2 1 3 1 5
Sample Output 1
11
The first color can paint cells 1,2,3, and the second color can paint cells 1,2,3,4,5.
There are 11 ways to paint that satisfy the condition, as follows:

Sample Input 2
3 3 1 1 2 2 3 3
Sample Output 2
1
The one way of not painting any cell satisfies the condition.
Sample Input 3
500000 10 1 499999 2 499998 3 499997 4 499996 5 499995 6 499994 7 499993 8 499992 9 499991 10 499990
Sample Output 3
775503999
Find the count modulo 998244353.